Dans cet article, on se propose de confirmer par le calcul que les transformations de Lorentz engendrent bien les trois effets contre-intuitifs présentés précédemment, à savoir:
- la fin de la simultanéité
- la contraction des longueurs dans le sens du mouvement
- la dilatation des durées
Nous avons montré qualitativement dans l'article Introduction à la fin de la simultanéité que deux évènements apparaissant comme simultanés dans un référentiel R donné ne l'étaient plus lorsqu'observés depuis un autre référentiel R' en mouvement rectiligne uniforme par rapport à R.
Montrons le désormais d'une manière plus algébrique à l'aide des transformations de Lorentz.
Deux évènements donnés E1(t1,x1,y1,z1) et E2 (t2,x2,y2,z2) dans R sont considérés comme simultanés et distants sur l'axe Ox si t1=t2 soit Δt=0 et x2-x1=Δx!=0
La règle des intervalles déduite précédemment dans la Remarque 2 de l'article Transformations de Lorentz I - Présentation nous donne, pour l'intervalle de temps Δt' séparant ces deux mêmes évènements dans le référentiel R':
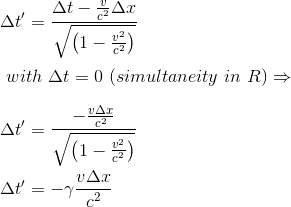
Cette équation représente une formulation algébrique de la relativité de la simultanéité entre référentiels.
Remarque 1: la simultanéité dans R' sera d'autant plus relative, c'est-à-dire que la différence de temps entre les deux évènements repérés dans R' sera d'autant plus grande que v, la vitesse relative des référentiels est élevée, et que la distance initiale entre les évènements est grande.
Remarque 2: pour de vitesse faibles par rapport à la lumière, donc dans un contexte de mécanique classique, on vérifie que Δt'=0; la simultanéité des évènements est conservée dans R'
L'on a déjà intuitivement montré que l'une des conséquences les plus célèbres de l'invariance de c est la contraction des longueurs, propriété selon laquelle tout corps en mouvement dans un référentiel inertiel R est contracté dans la direction de son mouvement d'un facteur γ = √(1-β2).
La contraction des longueurs dans la direction du mouvement se démontre facilement à partir de l'expression de la transformation de Lorentz en configuration standard, à condition de bien se souvenir que mesurer une longueur dans un référentiel donné signifie déterminer la distance entre les deux points à une date fixée dans ce référentiel.
La configuration la plus simple pour mettre en évidence cette contraction est de considérer deux repères inertiel R et R' avec R' se déplaçant dans la direction des x positifs avec une vitesse v. Dans une telle configuration, considérons à présent une règle rectiligne rigide alignée avec l'axe Ox, de longueur l0 au repos dans le référentiel R' ou elle est immobile, et telle que l'une de ses extrémités, notée A, coïncide avec l'origine O' du référentiel inertiel R'. Dans le référentiel R, à un instant t quelconque, ce même point A a pour coordonnées xA = vt, yA=0 et zA=0.
Il nous reste juste à déterminer les coordonnées de l'autre extrémité, B, au même instant t, grâce aux transformations de Lorentz en prenant en compte x'B=l0, y'B=0 et z'B=0 et d'en déduire la longueur l=xB - xA de la règle dans le référentiel R:
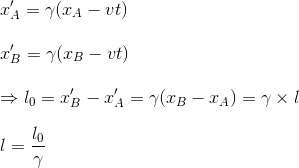
On confirme donc que la longueur de la règle dans le référentiel R où elle est mobile à la vitesse v est contractée d'un facteur γ par rapport a sa longueur au repos.
Il est en outre clair, d'après le principe de relativité, que la longueur, dans le système R, d'une règle de mesure l0, qui est au repos relativement à R' (calcul ci-dessus), doit être exactement la même que celle, dans le système R', d'une règle de mesure l0 qui est au repos relativement à R. Tâchons de montrer cela.
Pour connaître la longueur de la règle dans le référentiel R', il suffit de prendre un "instantané" à un instant t' donné, par exemple t'=0.
La première équation de Lorentz nous donne
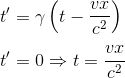
En remplaçant cette valeur dans l'équation relative aux abscisses, on peut exprimer les coordonnées des extrémités x'A et x'B de la règle dans le référentiel R' par rapport aux coordonnées de ces mêmes extrémités dans R. On a en effet:
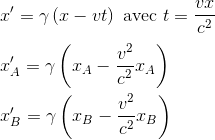
En nommant cette fois-ci l0 = xB-xA (longueur au repos dans R)
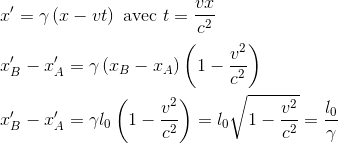
Une règle de longueur au repos l0 dans R est donc vue symétriquement raccourcie d'un facteur γ lorsqu'elle est vue depuis le référentiel R' en mouvement. CQFD.
On a vu qu'une autre conséquence importante des transformations de Lorentz est la dilatation des durées, principe qui énonce que toute horloge en mouvement dans un référentiel inertiel R semble, dans ce référentiel , évoluer au ralenti, à un rythme γ-fois plus lent.
La dilatation des durées est très simple à démontrer à partir des transformations de Lorentz, puisqu'elle consiste à comparer la durée écoulée entre deux événements dans un référentiel inertiel où ils ont lieu au même endroit (Durée propre), par exemple deux tic-tacs d'une horloge immobile, et dans un autre où ils se produisent en des endroits distants (durée impropre).
En notant Δt la première et Δt' la seconde, la transformation de Lorentz qui lie les deux référentiels implique ainsi directement, avec Δx = 0 (l'horloge étant immobile dans le référentiel R, les deux tic-tacs ont lieu à la même abscisse)
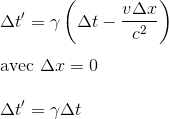
Remarque: Le caractère relatif du mouvement implique que cet effet, tout comme la contraction des longueurs vue précédemment, est lui aussi symétrique: si deux observateurs inertiels sont en mouvement l'un par rapport à l'autre, chacun considère que l'autre observateur vieillit au ralenti.
Montrons-le, c'est-à-dire explicitons à partir des mêmes équations le temps écoulé depuis une horloge immobile dans R' vu depuis le référentiel en mouvement R.
Une horloge immobile dans le référentiel R' donc avec pour différentielle de coordonnées Δx'=0, aura ses coordonnées dans R vérifiant la relation suivante Δx = Δvt
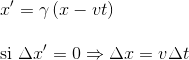
En injectant cette relation dans l'autre équation de Lorentz, qui donne t' en fonction de t et x, on obtient:
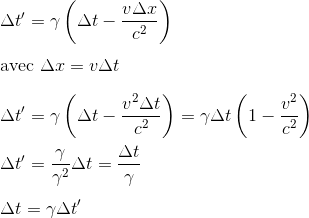
Vu depuis le référentiel R, puisque le facteur de Lorentz γ est toujours plus grand que un, le temps tel qu'il se passe dans R' semble se dilater; l'effet est bien symétrique.
CQFD.

