Le caractère relatif de la notion de simultanéité et l'invariance de c impliquent naturellement que la règle d'addition des vitesses galiléenne n'est plus valable en relativité restreinte.
Considérons un référentiel R, supposé au repos, et un référentiel R′ en translation uniforme par rapport à R à la vitesse V parallèlement à l'axe des abscisses.
Dans le référentiel R′, un mobile se déplace à la vitesse v'x. Quelle est la vitesse vx de mobile dans R?
La transformation de Galilée nous donne la loi d'addition des vitesses que l'on pratique intuitivement parce qu'elle correspond à notre experience quotidienne, conditionnée par des vitesses très faibles.
v'x = vx - v
Pour déterminer la loi qui la remplace, il suffit de considérer les différentielles des transformations de Lorentz en configuration standard. Pour décrire deux événements qui ont lieu sur l'axe x du référentiel R, on obtient pour les différentielles de coordonnées de ces mêmes événements repérés depuis R' en translation avec la vélocité v par rapport à R:
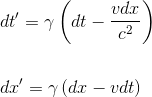
Si l'on divise la seconde équation par la première, on obtient:
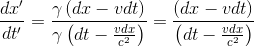
En divisant maintenant le numérateur et le dénominateur par l'intervalle infinitésimal dt:
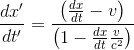
En revenant enfin à la définition des composantes cartésiennes de la vitesse vx=dx/dt et v'x=dx'/dt', on a finalement:
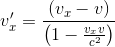 |
Par symmétrie, si l'on se place dans le référentiel R qui se déplace à la vitesse -V par rapport a R' parallèlement à l'axe des abscisses, l'on obtient:
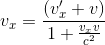 |
Soit un noyau radioactif se déplaçant à la vitesse v = 0.75c par rapport au référentiel du laboratoire. Il émet un électron qui possède lui-même une vitesse v'x=0.75c par rapport au noyau. La vitesse vx de l'électron dans le référentiel du laboratoire est alors égale à:
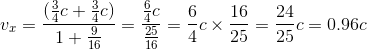
On confirme bien l'existence d'une vitesse-limite c quel que soit le référentiel considéré (en appliquant la règle galiléenne d'addition des vitesses, on aurait obtenu 0.75c+0.75c=1.5c comme vitesse par rapport au référentiel R du laboratoire, ce qui est impossible en relativité restreinte). Voir également la remarque 3 ci-dessous pour le cas limite de la vitesse de la lumière c dans le référentiel R' considérée depuis R.
Remarque 1: Dans le contexte relativiste, on parle plus de loi de composition de vitesses plutôt que de loi d'addition de vitesses (dont le champ d'application se limite à la mécanique classique)
Remarque 2: Dans le contexte de vitesses faibles par rapport a celle de la lumière (vx<<c et v<<c donc vxv<<c2) on retrouve la loi galiléenne d'addition des vitesses v'x = vx - v
Remarque 3: En gardant v comme vitesse relative de R' par rapport à R et c comme vitesse v'x de la lumière dans R', on vérifie que l'on conserve bien vx = c comme vitesse de la lumière dans R, et donc que c est constant et indépendant de la vitesse relative des référentiels:
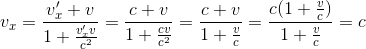
Remarque 4: En considérant également la définition des composantes cartésiennes de la vitesse vy=dy/dt, v'y=dy'/dt' et vz=dz/dt, v'z=dz/dt', on obtient également, toujours pour un mouvement relatif des référentiels sur l'axe Ox à la vitesse v:

où l'indice v sur le facteur de Lorentz souligne qu'il en dépend.
On note que bien que le mouvement relatif des référentiels R et R' s'effectue seulement le long de la direction x, les vitesses selon les axes y et z sont elles aussi affectées.
D'autre part, par définition, la direction θ, mesurée par rapport à l'axe Ox dans laquelle se dirige un corps mobile à la vitesse v dans un plan xOy vérifie tanθ = vy/vx. On en déduit donc de la formule de composition des vitesses que, tout comme en physique newtonienne, la direction du mouvement d'un corps dépend du référentiel, la relation entre les tangentes des angles mesurés dans R et R' s'écrivant:
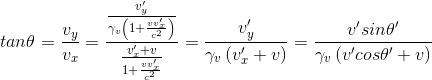
Remarque 5: Cette équation permet d'expliquer l'aberration de la lumière. En effet, si l'on suppose une étoile située orthogonalement au plan elliptique dans le référentiel héliocentrique R' (θ'=π/2), pour un observateur terrestre (lié au référentiel R), le rayon lumineux provient d'une direction qui fait un angle θ donné par tanθ = c/v (sinθ'=1, cosθ'=0 et γv proche de 1 puisque vitesse de rotation de la Terre en orbite autour du Soleil = 30km/s négligeable en relativité). L'angle donné par rapport à la verticale de ce plan est π/2-θ donc le rayon lumineux semble provenir d'un angle θvertical avec la verticale tel que θvertical = tan-1(π/2-θ)=v/c. L'amplitude du mouvement d'aberration est donc environ de 

