Dans cet article, nous allons montrer qu'il est possible de déduire très simplement les équations de Lorentz à partir du principe de relativité et de la constance de la vitesse de la lumière dans le vide.
Nous reproduisons ici de façon un peu plus détaillée le raisonnement tel que présenté par Einstein dans son ouvrage La relativité, dans l'appendice 1[1].
Soit deux référentiels inertiels R et R' en configuration standard, en translation uniforme le long des axes des abscisses. Limitons-nous dans un premier temps à des évènements localisés sur l'axe des x. Un tel évènement est représenté, relativement à R, par l'abscisse x et le temps t, et relativement au référentiel R' par l'abscisse x' et le temps t'. Notre problème consiste donc à trouver x' et t' quand x et t sont donnés.
1. Application du postulat de la constance de la vitesse de la lumière dans tout référentiel
Un rayon lumineux qui avance le long de l'axe positif des x se propage d'après l'équation x= ct soit encore x - ct =0. Mais puisque le même rayon lumineux se propage relativement à R' avec la même vitesse c, l'équation de sa propagation dans R' sera x' - ct' =0. L'annulation de la quantité x - ct entraînant celle de x' - ct' , on doit avoir une relation du type
x' - ct' = λ (x - ct) (1)
Un raisonnement analogue appliqué à des rayons lumineux se propageant dans la direction des x négatifs entraîne la condition
x' + ct' = μ (x + ct) (2)
En additionnant et en soustrayant les équations (1) et (2), et en utilisant, au lieu des constantes λ et μ, les constantes:
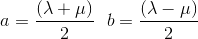
on obtient:
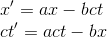
Par ailleurs, le fait que l'origine O' du référentiel R', ait pour coordonnées permanente x'=0, nous donne:
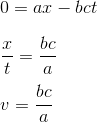
avec donc v=bc/a la vitesse relative des deux référentiels inertiels R et R'.
2. Application du caractère relatif du mouvement entre référentiels inertiels
Après avoir appliqué le principe de la constance de la vitesse dans tout repère inertiel, nous allons maintenant appliquer le second postulat de la relativité qui pose le caractère relatif du mouvement, en l'occurrence que la contraction de longueur est symétrique: si un corps immobile dans un référentiel R' est contracté dans un référentiel R par rapport auquel il est mouvement, il en est de même de tout objet immobile dans R quand il est étudié depuis le référentiel R' en question.
Pour cela, nous pouvons applique exactement le même raisonnement que celui mené dans l'article Transformations de Lorentz II - Cinématique relativiste- Contraction des longeurs et dilatation des durées, onglet Contraction des longueurs.
Si nous voulons déterminer la longueur d'une règle de longueur unité dans R' depuis R, on choisit un "instantané" à l'instant t=0 dans R:
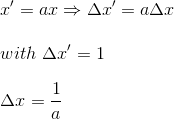
Si l'on veut exprimer de manière symétrique la longueur depuis R' de la règle de longueur unité dans R, il suffit cette fois-ci de choisir un instantané à l'instant t'=0, ce qui nous donne l'équation t=bx/ca que l'on réinjecte ensuite dans l'équation x'=ax-bct:
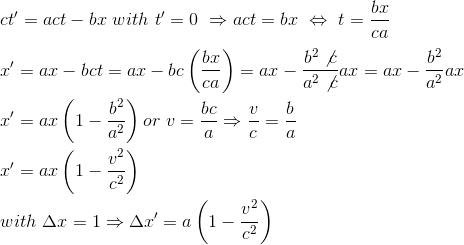
L'égalité des deux équations précédentes, i.e la longueur de la règle observée depuis le référentiel en mouvement R égale la longueur de la règle observée depuis le référentiel en mouvement R', on a:
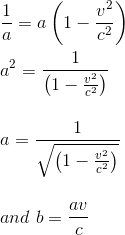
En remplaçant ces valeurs dans nos équations originales, on trouve:
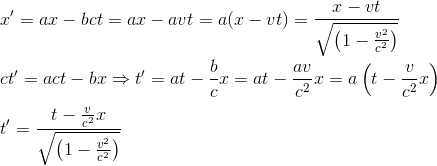
On vient d'obtenir la transformation de Lorentz pour des événements situés sur l'axe x. L'extension de ce résultat à des évènements quelconques, c'est-à-dire ayant lieu également en dehors de l'axe des abscisses est obtenue en ajoutant les relations
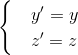
En effet, si l'on considère un photon émis à l'origine de R à l'instant t=0, moment où les deux origines coïncidaient, ses coordonnées spatiales et temporelles dans les deux référentiels doivent, en raison de l'invariance de la vitesse de la lumière dans le vide, vérifier:
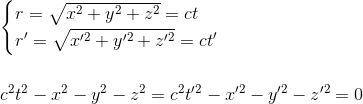
On vérifie qu'avec c2t2 - x2 = c2t'2 - x'2 donné par les expressions de x' et t', cette dernière égalité de vitesse de photons dans les deux référentiels ne peut être vraie que si y'=y et z'=z.
CQFD.
[1] Dérivation simple de la transformation de Lorentz (Complément du Chapitre 11) La relativité Petite Bibliothèque Payot pp.163

