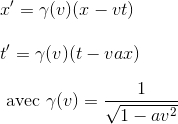Dans l'article précédent Transformation de Lorentz IV - Dérivation, nous avons montré de quelle façon Einstein a pu dériver les transformations de Lorentz, à partir des deux postulats de la relatvité restreinte que sont le principe de relativité et la constance de la vitesse de la lumière.
En fait, comme l'a montré J.M Levy-Leblond dans son article Une dérivation de plus des transformations de Lorentz, le second postulat (invariance de c) n'est pas nécessaire pour obtenir la loi de transformation de Lorentz. Le principe de relativité, accompagné de l'hypothèse de certaines symétries de l'espace-temps, suffit à lui seul. Le principe de relativité se traduit mathématiquement par le fait que les lois de la nature doivent garder la même forme quel que soit le système de coordonnées choisi lorsqu'on passe d'un référentiel d'inertie à un autre. Avec ces seules conditions, les lois de transformations les plus générales des systèmes de coordonnées doivent posséder une structure de groupe. Et la constante c qui joue le rôle de vitesse limite dans les lois de transformations générales n'apparait pas nécessairement comme devant être la vitesse de la lumière. Cette constante est égale à la vitesse de la lumière seulement si le photon possède une masse nulle (ce qui est a priori le cas).
Sans surprise, on commence par considérer deux référentiels R et R' en translation uniforme l'un par rapport à l'autre suivant l'axe des x, en posant (x,t) les coordonnées dans le premier et (x',t') les coordonnées dans le second.
On part de l'hypothèse suivante:
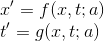
où a est un paramètre indéfini qui distingue le référentiel R' du référentiel R et f et g sont des fonctions inconnues qu'il nous reste à déterminer.
Hypothèse 1: espace-temps homogène
Si on suppose que l'espace-temps est homogène, c'est-à-dire qu'il a partout et toujours les mêmes propriétés, alors les lois de transformation ne dépendent pas de la position spatio-temporelle. Dit autrement encore, cela signifie que les coefficient de dx et dt dans les équations différentielles suivantes doivent etre indépendants de x et t,
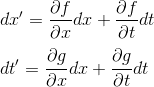
et donc que f et g sont des fonctions linéaires de x et t. On peut donc écrire:
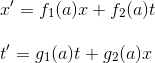
L'origine O' de R', de coordonnées x'=0 se déplaçant à la vitesse V par rapport à R, l'équation ci-dessus conduit à V=-f2(a)t/f1(a)t. V est donc une fonction de a qui peut être, tout comme le paramètre a, utilisée pour caractériser les référentiels. C'est évident puisque seule la vitesse relative distingue R de R'. On réécrit alors notre équation en fonction du paramètre V
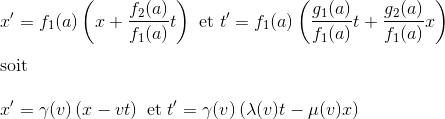
avec désormais les trois fonctions γ(v), λ(v) et μ(v) à déterminer.
Hypothèse 2: isotropie de l'espace
L'hypothèse d'isotropie de l'espace impose que l'orientation des axes des référentiels sont physiquement indépendantes. Conséquemment, la transformation représentant le passage de R à R' doit présenter la même forme que celle représentant le passage de r(R) à r(R') où l'opérateur r correspond à une réflexion, c''est-à-dire à un changement de x en -x et de x' en -x'. Dans cette opération, puisque le sens des axes change, la vitesse de r(R') par rapport à r(R) vaut donc -V. On a donc:
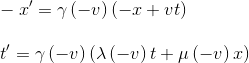
En comparant les deux dernières équations, on obtient:
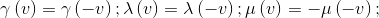
Hypothèse 3: loi de Groupe
L'équivalence entre référentiels galiléens se traduit mathématiquement par la structure de groupe des transformations recherchées.
En particulier, la transformation de R en R' doit avoir la même forme que la transformation de R' en R en changeant V en -V. Ce qui conduit, à partir de l'équation initiale déduite de l'hypothèse 1 de l'espace-temps homogène:
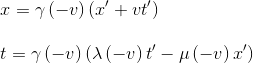
soit en utilisant les égalités sur les fonctions γ(v), λ(v) et μ(v) déduites de l'hypothèse 2 de l'isotropie de l'espace:
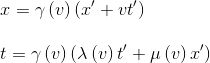
En utilisant à nouveau les expressions de x' et t' données initialement par l'hypothèse 1, et en les remplaçant dans la nouvelle expression de x ci-dessus, il s'ensuit:
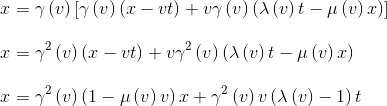
Pour que cette égalité soit vérifiée, quelles que soient les valeurs de x et t, il faut avoir:
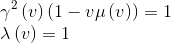
En remplaçant ces égalités dans nos équations de l'hypothèse 1, on obtient:
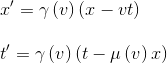
Restent donc à déterminer γ(v) et μ(v), sachant que ces fonctions sont liées entre elles par la première égalité déduite plus haut en même temps que λ(v)=1.
Pour cela, nous pouvons utiliser la propriété de la loi de composition interne: la composée de deux transformations doit avoir la même forme que chacune des transformations. Soient donc R,R' et R'' trois référentiels galiléens. Soient V1 la vitesse de R' par rapport à R et V2 la vitesse de R'' par rapport à R'.
On a entre R' et R'':
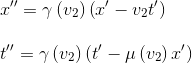
En remplaçant à leur tour x' et t' par leurs expressions:
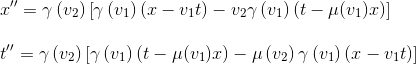
ce que l'on peut réécrire sous la forme
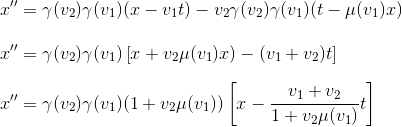
et
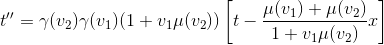
Soit V3 la vitesse de R'' par rapport à R, on peut également écrire directement la transformation de R à R'' sans passer par R':
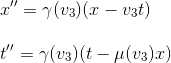
Dans les dernières équations, on constate que le coefficient de x dans l'expression de x'' est identique à celui de t dans l'expression de t'' et égal à γ(v3). On se sert de cette remarque aux équations trouvées juste avant, et on en déduit:
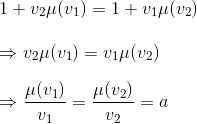
Ce dernier rapport est une constante puisque les vitesses v1 et v2 sont choisies de manière arbitraire. On nomme a cette constante pour la suite.
En comparant les deux expressions x'' , on peut en déduire:
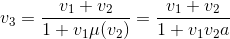
avec, en reprenant l'equation de γ en fonction de v et μ(v):
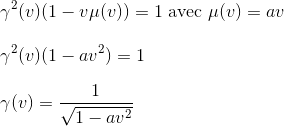
On choisit la racine positive pour avoir γ(0)=1 dans la limite des vitesses faibles.
On obtient donc à ce stade: