Dans cet article notre but est d'illustrer par les diagrammes d'espace-temps ce que l'on avait déjà présenté intuitivement et qualitativement dans notre article précédent Introduction à la fin de la simultanéité: deux événements simultanés dans un référentiel R ne le sont plus dans un référentiel R' en mouvement rectiligne uniforme par rapport à R.
On reprend l'exemple des deux horloges au repos dans un même référentiel mais non situées au même endroit.
On se rappelle que l'astuce pour s'assurer que deux horloges A et B sont synchronisées consiste à introduire une troisième horloge/personne C à mi-chemin entre A et B. Au moment précis où l'horloge marque midi, elle envoie un flash lumineux vers C. De même quand B marque midi, elle envoie aussi un flash vers C. Puisque la vitesse de la lumière est la même pour chaque flash et que les distances à parcourir AC et CB sont identiques, ils mettront le même temps pour arriver à C. Nous disons que les deux horloges sont synchronisées si et seulement si elles arrivent les deux flashs parviennent en C en même temps.
Plaçons-nous à présent dans le référentiel du bonhomme se déplaçant vers la gauche en bas du diagramme. Pour lui, les trois horloges se déplacent vers la droite avec une vitesse v et avec, si l'on prend par exemple un écart de 1 unité entre chaque horloge, les trois équations de mouvement des horloges sont les suivantes, avec x et t les coordonées dans le référentiel de l'observateur et x' et t' les coordonnées dans le référentiel où les horloges sont au repos:
- - horloge A : x = vt (x' = x - vt =0)
- - horloge C : x = vt + 1 (x' = x - vt =1)
- - horloge B : x = vt + 2 (x' = x - vt = 2)
En effet, le référentiel de l'horloge A se déplace de telle sorte que x'=x-vt et l'on suppose que A est immobile et positionné à l'abscisse 0 de son référentiel R'.
L'horloge B est animée de la même vitesse v que l'horloge A dans le référentiel de l'observateur mais a une absisse x'=1 soit x-vt=1 et C reste à la position fixe x'=2 soit x-vt = 2
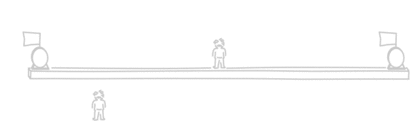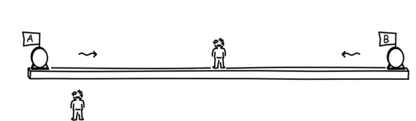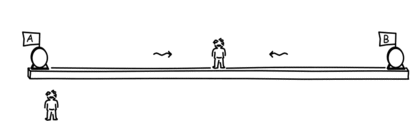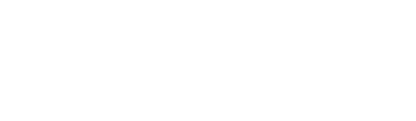
Supposons que l'horloge A envoie depuis l'origine (x=0, t=0, x'=0, t'=0) un signal lumineux à l'horloge B. L'horloge C le verra au point x sur le diagramme espace-temps ci-dessous, puisque la ligne d'univers de tout signal lumineux envoyé par A doit faire un angle de 45 degrés par rapport à l'axe x (on suppose communément la vitesse de la lumière c=1 en prenant la seconde comme unité de temps et la seconde lumière comme unité de longueur)
A quel moment B doit-il envoyer un signal à C pour qu'il le reçoive au même moment? Nous pouvons le découvrir restrospectivement facilement : il nous suffit simplement de dessiner le segment de droite partant de x, incliné de 45 degrés vers le bas et la droite, jusqu'à ce qu'il croise la ligne d'univers de B. Il s'agit du point y dessiné ci-dessous.
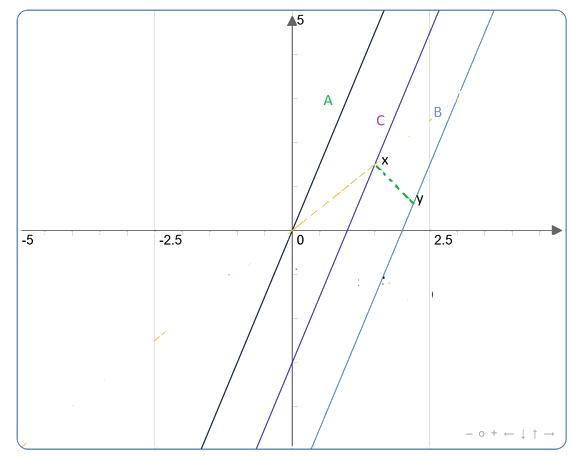
Ce que nous venons de montrer, c'est que l'origine et le point y sont des événements simultanés dans le référentiel en mouvement constitué des trois horloges mais ne sont plus du tout simultanés dans le référentiel considéré au repos de l'observateur.
En effet, les points origine et y ne sont plus du tout situés sur la même hauteur sur le diagramme et ils correspondent donc à des temps dans le référentiel au repos t=0 et t=ty distincts et ty> 0!
CQFD.
Remarque: en effet, vu du référentiel du bonhomme, les horloges se déplacent vers la droite, avec la lumière émise par l'horloge A ayant à parcourir une plus grande distance que celle émise par l'horloge B pour arriver au centre de la plateforme (le centre de la plateforme fuit la lumière émise par A et au contraire va à l'encontre de la lumière émise par B à vitesse constante).

Ayant à parcourir une plus grande distance à la même vitesse, la lumière émise par A doit nécessairement mettre plus de temps, et donc a nécessairement été émise avant la lumière émise en B; ce que confirme sur notre schéma ty (instant de l'émission par B) supérieur à 0 (instant de l'émission par A)
Et d'après les équations de Lorentz telles que présentées dans notre article Transformations de Lorentz II - Cinématique relativiste- Contraction des longeurs et dilatation des durées, on est même capable de quantifier précisément cet écart de temps:
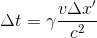
En résumé: Dans le référentiel des horloges, les deux horloges A et B sont synchronisées, c'est-à-dire émettent le signal lumineux en même temps avec chacune des horloges marquant midi.
Dans le référentiel du bonhomme, les deux horloges A et B ne sont plus synchronisées: au moment où l'horloge A marque midi et envoie le signal lumineux vers C, l'horloge B n'a pas encore envoyé son signal et marque (midi - Δt) tel que défini plus haut. L'horloge B retarde par rapport à l'horloge A d'un intervalle de temps Δt.

