Le phénomène d'aberration de la lumière, également connu sous le nom d'aberration stellaire, a été mis pour la première fois en évidence, dans un cadre non relativiste, par l'astronome britannique James Bradley (1693-1762) en observant la position de γ Draconis.
L'observation que fit Bradley était qu'au cours de l'année les étoiles ont un mouvement apparent elliptique, ce qu'il interpréta comme le résultat de la composition du mouvement de la Terre sur son orbite avec celui de la lumière en provenance d'étoiles.
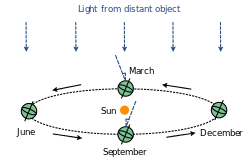
En effet, par analogie avec le cas d'un automobiliste se déplaçant sous la pluie et qui semble la voir venir frapper de façon oblique le pare-brise alors qu'elle tombe verticalement[1], un observateur terrestre n'observe pas une étoile dans la direction où elle est réellement car d'une part la vitesse de la lumière est finie et d'autre part, la Terre se déplace autour du Soleil à une certaine vitesse[2].
Plus précisément, un rayon lumineux qui atteint le plan de l'écliptique orthogonalement dans le référentiel héliocentrique semble provenir, pour un observateur terrestre, d'une direction qui fait un angle α avec la verticale à ce plan, donné par tan α ≈ α ≈ v/c ≈ 10-4 radians.
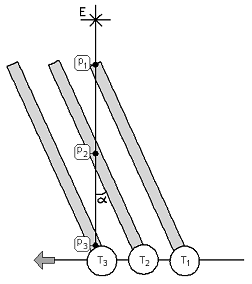
Si l'on regarde le dessin ci-contre qui montre un téléscope pointé sur une étoile E située exactement au-dessus de la tête de l'astronome en plein mois de septembre (position E).
À l'instant T1, la lumière de l'étoile arrive au niveau de l'objectif du télescope. À T2, la lumière a parcouru la moitié du tube du télescope, mais pendant ce temps, à cause de la vitesse de la Terre autour du Soleil, le télescope a bougé vers le gauche.
On se rend bien compte que si le télescope avait été dirigé exactement vers la position réelle de l'étoile, alors la lumière de l'étoile serait venue frapper la partie intérieure droite du télescope et ne serait jamais donc arrivée jusqu'au fond...
La lumière, finalement arrive au niveau de l'oculaire du télescope au temps T3, et on voit que le télescope pointe en fait vers une position observée de l'étoile qui n'est pas la position réelle[3].
Essayons de calculer cet angle:
Entre T2 et T3, la Terre a parcouru une distance ΔdT =v.Δt=29.86 × (T3-T2)
Entre T2 et T3, la lumière a parcouru une distance ΔdL=c.Δt =300000 × (T3-T2)
et donc
tan(α) = distance parcourue par la Terre / distance parcourue par la lumière = v/c = 29,86/300000 soit finalement
α = tan-1(29,86/300000) = 0,0057°= 20,53''
Remarque 1: L'aberration changeant de sens tous les six mois du fait du mouvement de laTerre autour du Soleil, le mouvement apparent circulaire de l'étoile se fait avec une ouverture angulaire de 2α = 41'', en accord avec les observations de Bradley.
Remarque 2: L'analyse fine de ses observations révéla à Bradley que l'angle d'aberration était le même pour toutes les étoiles, ce qui n'était possible que si les rayons reçus avaient la même vitesse par rapport à la Terre, et que cette vitesse ne dépendait pas du mouvement de leur source.
Remarque 3: L'angle de l'aberration stellaire peut être également retrouvé par la formule de l'addition des vitesses en mécanique classique ou par la loi de la composition des vitesses en relativité, comme on l'a montré dans l'article Transformations de Lorentz III - Cinématique relativiste - Composition des vitesses. Dans la formule suivante, il suffit de choisir l'angle θ'=π/2 (lumière arrivant orthogonalement) et v'=c
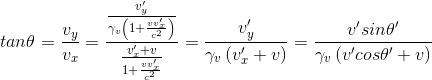
Dans la limite newtonienne, où v<<c on a γv≈1 et tan(θ'-θ) = tan(π/2-θ) ≈ 1/tanθ ≈ v/c
[1] La légende veut que Bradley eut quant à lui l'idée de cette analogie après avoir observé la modification d'orientation d'un drapeau flottant au vent sur un bateau en mouvement sur la Tamise.
[2] qui vaut environ 30km/s, comme on le sait à présent.
[3] Si l'observation avait été faite au mois de mars, pendant que la Terre se dirige exactement dans l'autre sens, alors le décalage aurait été inverse.

