Il existe une famille d'observateurs pour lesquels le principe d'inertie, dit aussi principe de Galilée ou première loi de la dynamique, est valable.
Selon ce principe, dans le référentiel associé à un tel observateur, la vitesse du centre de la masse de tout système isolé - c'est-à-dire qui n'est soumis à aucune action extérieure est constante.
Les référentiels pour lesquels ce principe sont naturellement nommés référentiels galiléens ou inertiels.
Une propriété fondamentale des référentiels inertiels, qui reste valable en relativité restreinte, est qu'ils sont tous en en translation rectiligne uniforme les uns par rapport aux autres. Il n'y a donc ni accélération relative de leurs origines, ni rotation relative de leurs bases.
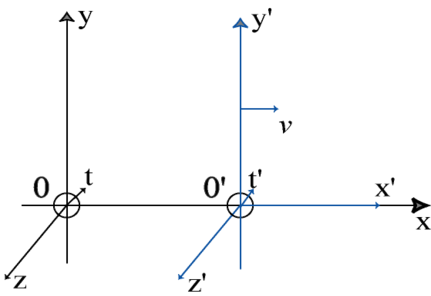
Étant donné deux observateurs inertiels en mouvement relatif à la vitesse v, on choisit souvent leurs référentiels respectifs en configuration standard, c'est-à-dire que:
- - les origines sont confondues à l'instant initial
- - les vecteurs de base sont identiques, ou, de manière équivalente, les axes associés aux référentiels sont parallèles
- - le vecteur vitesse vR'/R = v est colinéaire avec la droite Ox qui est confondue avec O'x'
Remarque: Une autre manière avancée de caractériser le mouvement d'un observateur inertiel comme déplacement en ligne droite, à vitesse constante est de le spécifier comme la ligne d'univers de temps propre maximal entre deux évènements donnés - pour plus de détails, voir l'article Geodesics as proper time maximization, non encore traduit en français. Dit encore autrement, parmi toutes les trajectoires possibles, une particule libre se déplacera toujours le long d'une trajectoire telle qu'elle vieillira le plus le long de cette trajectoire.

