Transformations de Lorentz I - Présentation

       Comme expliqué précédemment, l'invariance de la vitesse de la lumière dans le vide, c, mena Einstein à se poser la question suivante:

"Peut-on concevoir entre le lieu et le temps des événements, par rapport à deux corps de référence inertiels, une relation telle que tout rayon lumineux possède la même vitesse de propagation c par rapport à chacun de ces référentiels?"^[1]

Cette question le conduisit à une réponse affirmative "tout à fait certaine" et à une loi de transformation des grandeurs spatio-temporelles d'un évènement quand on passe d'un référentiel à un autre, exprimée sous la forme des transformations de Lorentz.^[2]

Avec (x,y,z,t) et (x',y',z',t') les trois coordonnées spatiales et temporelle permettant de repérer un même évènement depuis deux référentiels inertiels R et R' en translation rectiligne uniforme l'un par rapport a l'autre en configuration standard, i.e.:

• - les origines sont confondues à l'instant initial
• - les vecteurs de base sont identiques, ou, de manière équivalente, les axes associés aux référentiels sont parallèles
• - le vecteur vitesse v_R'/R = v est colinéaire avec la droite Ox qui est confondue avec O'x'

alors les transformations de Lorentz s'écrivent:

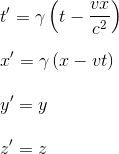avec γ (lettre grecque minuscule gamma), appelée Facteur de Lorentz (Lorentz factor en anglais), déja introduite dans l'article précédent Introduction à la dilatation des durées et au facteur de Lorentz et définie de la manière suivante:

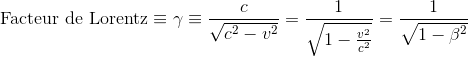
en posant par convention β = v/c.

Remarque 1: Conformément au principe de relativité, il n'existe pas de référentiel inertiel privilégié de telle sorte que les transformations de coordonnées entre le référentiel R et R' prennent exactement la même forme que les transformations de R' vers R. La différence étant que le vecteur vitesse v doit être changé en -v étant donné que si R' se déplace suivant le vecteur vitesse v par rapport à R, alors R se déplace avec le vecteur vitesse opposé -v par rapport à R'. Si un observateur en R' enregistre un événement avec les coordonnées (t',x',y',z'), alors un observateur se déplaçant avec une vitesse -v par rapport à R' enregistrera le même évènement en R selon les coordonnées (t,x,y,z) ainsi définies:

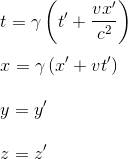Remarque 2: Les transformations de Lorentz étant linéaires par rapport aux variables xⁱ et t, il existe des égalités semblables si l'on considère deux événements A et B distincts, de coordonnées séparées par (Δt,Δx,Δy,Δz) dans un référentiel inertiel R, et par (Δ't,Δx',Δy',Δz') dans un autre référentiel R'. On a en effet:

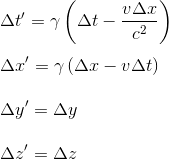Remarque 3: Les formules des transformations de Lorentz peuvent s'approximer dans le cas où la vitesse v du référentiel en mouvement est petite devant celle de la lumière. En négligeant le terme v/c dans les formules, on retrouve alors les transformations de Galilée, c'est-à-dire les transformations correspondantes aux changements de référentiel en mécanique classique.

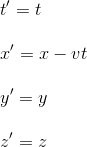
Remarque 4: Il convient enfin de vérifier que conformément au second principe de la relativité restreinte, la vitesse de la lumière reste inchangée entre observateurs inertiels.

Pour cela, considérons un rayon de lumière envoyé à l'instant t=0 parallèlement à l'axe des abscisses, dans la direction des x positifs. Dans le référentiel R, l'équation de du mouvement de ce rayon lumineux s'écrit simplement x = ct c étant la vitesse de la lumière dans le vide. En remplaçant cette valeur dans les équations de Lorentz, on peut écrire les coordonnées x' et t' de ce rayon dans le référentiel R':

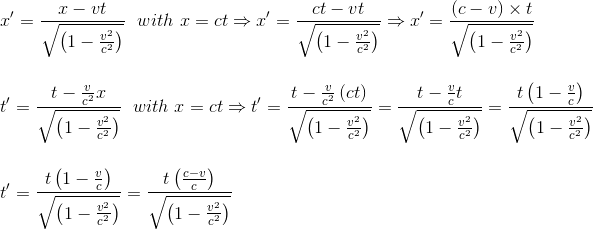
 Déterminer la vitesse de ce rayon lumineux dans le référentiel R' en mouvement par rapport à R est alors évident, v' = x'/t'=c:

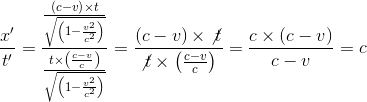
On vient de vérifier que la vitesse de la lumière demeure invariante par transformation de Lorentz.

Remarque 5: Pour une valeur v>c, on remarque le facteur de Lorentz prend une valeur imaginaire, d'où il résulte que les équations de Lorentz n'ont de sens que si nous donnons à v une valeur inférieure à c; la vitesse c comme vitesse limite résulte déjà des équations mêmes des transformations de Lorentz.

[1] Albert Einstein La relativité  - Chapitre 11 Les transformations de Lorentz. Dans son exemple, Einstein choisit comme référentiels inertiels un train et un talus en translation uniforme l'un par rapport à l'autre.

[2] C'est Henri Poincaré qui en 1905, présentant à l'Académie des Sciences la note Sur la dynamique de l'électron résumant son article qu'il prévoit de présenter à Palerme, confirme et corrige les résultats de Lorentz de 1904, et leur donne leur nom définitif de 'transformations de Lorentz'.