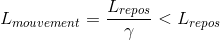Une autre conséquence directe de l'invariance de c est la contraction des longueurs, propriété que l'on pourrait définir de la façon suivante:
|
Tout corps en mouvement à la vitesse v<c dans un référentiel ℜ est contracté dans la direction de son mouvement d'un facteur √(1-β2) = 1/γ avec β = v/c |
Pour démontrer cela, considérons un vaisseau en train de se déplacer de la Terre vers Jupiter en ligne droite et à vitesse v constante, par rapport à la Terre et à Jupiter.
Admettons également que cette distance reste rigoureusement constante de sorte que l'ensemble Terre+Jupiter constitue un référentiel d'inertie, de même que le vaisseau en mouvement par rapport au référentiel Terre + Jupiter.

Connaissant la vitesse du vaisseau, la distance se déduit par le calcul de la durée du voyage du vaisseau, c'est-à-dire encore par la durée entre les deux événements suivants:
- - évènement 1: le vaisseau passe à la hauteur de la Terre
- - évènement 2: le vaisseau passe à la hauteur de Jupiter
Référentiel du vaisseau
Depuis le référentiel du vaisseau, une seule horloge est nécessaire puisque chaque événement a lieu à proximité du vaisseau: il s'agit donc d'une durée propre ΔT0.
La longueur Terre-Jupiter dans ce référentiel est donc L = v x ΔT0
Référentiel terrestre
Pour nous, sur Terre, les deux événements ne se produisent pas au même endroit. Deux horloges synchronisées doivent être installées, une première horloge sur Terre afin de repérer le premier événement (vaisseau au dessus de la Terre) et une seconde afin de marquer le second évènement (vaisseau au-dessus de Jupiter). Nous mesurons manifestement une durée impropre ΔT.
Dans le référentiel terrestre, la longueur au repos entre la Terre et Jupiter est égale à L0 = v x ΔT
Rapport entre les longueurs
En comparant la vitesse relative v dans les deux équations, on a:
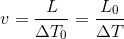
En reprenant l'équation de dilatation entre temps impropre et temps propre vue précédemment dans Introduction à la dilatation des durées et au facteur de Lorentz, on peut écrire:
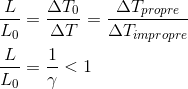
Dans le référentiel de l'astronaute, la longueur (L en mouvement) est plus courte que dans le référentiel terrestre (longueur L0 au repos)
|
Une longueur est plus courte dans un référentiel par rapport auquel elle est en mouvement, que dans un référentiel par rapport auquel elle est au repos |
Remarque 1: La longueur dans le référentiel ℜ où elle est en mouvement à la vitesse v est L0/γ uniquement si la vitesse est colinéaire à la longueur: dit autrement, il n'y a que les longueurs parallèles au vecteur vitesse qui dépendent du référentiel dans lesquelles on les mesure (dans l'article précédent, la hauteur L de l'horloge lumineuse était la même dans les deux référentiels).
Remarque 2: il découle de la remarque ci-dessus que pour un objet "tridimensionnel", il n'y a contraction que dans la direction de son mouvement, ce qui implique que son volume est lui aussi réduit d'un facteur γ.
Remarque 3: la contraction des longueurs ne permet pas de décrire l'apparence visuelle d'un objet en mouvement à une vitesse proche de c, mais uniquement la forme qu'il aurait si l'on procédait à une mesure instantanée, dans le référentiel où il est mobile, de ses propriétés géométriques. En effet, pour déterminer ce à quoi il ressemble si on le regarde, il faut également prendre en compte le fait que la lumière qu'il émet doit parvenir à l'observateur. L'objet tel qu'il est vu, et non pas mesuré, semble en général avoir subi plutôt qu'une contraction nette, une sorte de rotation et une déformation d'autant plus importantes qu'il est proche: ce sont les conséquences de l'effet Lampa-Terrel-Penrose.