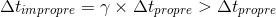Une autre conséquence importante du principe de l'invariance de la vitesse de la lumière est celle de la dilatation des durées. Ce concept peut s'énoncer de la manière suivante:
|
Toute horloge en mouvement à la vitesse v<c par rapport à un référentiel inertiel R semble, dans ce référentiel, évoluer au ralenti, à un rythme γ-fois plus lent. γ étant défini comme le facteur de Lorentz et valant 1/√(1-β2) avec β=v/c |
Pour mettre en évidence cet effet, nous allons considérer une "horloge lumière", où une impulsion lumineuse effectue des va-et-vient entre deux miroirs parallèles distants d'une longueur L.

Référentiel au repos
Par une expérience de pensée, embarquons cette horloge dans un vaisseau en mouvement rectiligne
uniforme de vitesse v par rapport à la Terre. Supposons en plus que la
vitesse soit perpendiculaire au tube de l'horloge.
Dans ce référentiel, soit pour un astronaute situé dans le vaisseau, la lumière se déplace verticalement, de bas en haut et de haut en bas. Mesurons à présent l'intervalle de temps entre les événements "le signal part du
miroir inférieur" et "le signal est reçu par le miroir inférieur".
Cette durée peut être facilement calculée comme le rapport T entre deux fois la distance entre les miroirs, soit 2xL divisée par la vitesse de la lumière (supposée ici être celle de la lumière dans le vide).
Assumons par exemple que les miroirs soient séparés d'une distance d'un mètre, alors il faudra à la lumière 6.67 nanosecondes pour faire une aller-retour entre les deux miroirs, ce qui en fait une horloge de très haute précision (150 millions tics par seconde).
Qu'observons-nous sur Terre?
Pour nous, c'est-à-dire pour un observateur immobile sur la Terre[1], l'horloge est en mouvement uniforme de vitesse v et le signal parcourt une distance plus longue. D'après le second postulat, la vitesse du signal lumineux est pour nous également c. Il met donc un temps T'>T pour parcourir la distance D>L entre les deux miroirs.
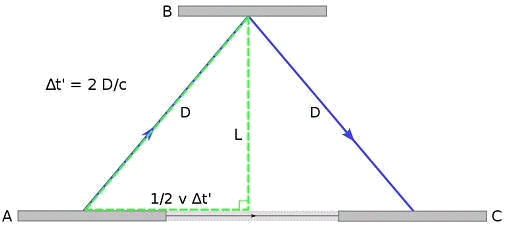
La durée Δt' mise par la lumière pour faire un aller-retour est donc désormais:
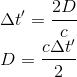
En utilisant le théorème de Pythagore pour le triangle vert, la longueur de la base représentant la moitié de la distance parcourue par le vaisseau pendant la durée Δt'
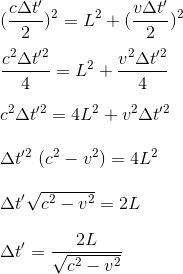
En se rappellant que la durée mis par la lumière dans le référentiel du vaisseau pour faire un aller-retour est de:
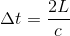
Alors le rapport entre les deux durées nous indique de quel facteur le temps observé par l'observateur dans le référentiel terrestre se trouve modifié par celui mesuré par l'astronaute dans son propre référentiel:
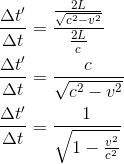
Si l'on nomme β le rapport entre la vitesse relative des deux référentiels et la vitesse de la lumière
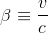
Le rapport des durées peut se réécrire sous la forme courante suivante:
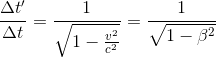
La quantité à droite de l'équation représente une quantité très fréquemment rencontrée en relativité restreinte: il s'agit du facteur de Lorentz (Lorentz factor en anglais) que l'on représente par la lettre grecque gamma, notée γ
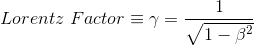 |
On constate que puisque la vitesse relative v des deux référentiels doit être inférieure à la vitesse limite c, on a γ>1 et donc dans le référentiel terrestre l'intervalle de temps Δt' est supérieur à celui Δt enregistré dans le référentiel de l'astronaute. En termes simples, l'horloge en mouvement, ici celle de l'astronaute dans son vaisseau spatial, retarde par rapport à celle de l'observateur fixe sur Terre.
Si nous appelons intervalle de temps propre la durée entre deux événements se produisant au même lieu de l’espace, cet intervalle étant mesuré par une seule horloge se trouvant à l’endroit où les événements se produisent et intervalle de temps impropre la durée entre deux événements se produisant en des lieux différents, cet intervalle ne pouvant être mesuré que par deux horloges se trouvant aux deux endroits où les événements se produisent, le principe de dilatation des durées peut s'énoncer de la façon générale suivante:
|
Deux horloges A et B séparées dans l'espace, enregistrent entre deux événements un intervalle de temps (impropre) plus grand que l'intervalle (propre) enregistré par une seule horloge se déplaçant de A vers B, et qui est présente aux deux événements.
|
Remarque 1: Si dans l’expérience de pensée précédente, l’astronaute examine notre "horloge à lumière" (en mouvement pour lui), il doit aboutir à la même conclusion, c'est-à-dire que notre horloge en mouvement marche plus lentement que la sienne au repos. Les effets de dilatation de temps sont parfaitement symétriques par rapport à chaque référentiel inertiel.
Remarque 2: Nous avons pris l'exemple d'une horloge à lumière pour mettre en évidence le phénomène de dilatation de temps car nous avons pu utiliser directement le postulat de la relativité selon lequel la vitesse de la lumière est identique dans tous les référentiels inertiels, mais il faut se convaincre que l'ensemble des phénomènes temporels, gestes quotidiens, mouvements mécaniques de machines, battements du cœur et autres phénomènes physiologiques, etc., tout se déroule au ralenti. De même pour l’astronaute observant l’observateur terrestre. Supposons en effet un moment que le ralentissement du temps n'affecte que les horloges à lumière et non les autres types de montre. Si cela était le cas, alors il serait possible à l'observateur situé dans le vaisseau de remarquer que dans son référentiel, une horloge à lumière marche au ralenti par rapport à une montre classique, et donc de trouver un critère suffisant pour remarquer qu'il est en mouvement. Cela heurterait de plein fouet le postulat de l'équivalence des lois de la Nature entre référentiels inertiels qui, formulé d'une manière plus commune, exprime qu'il est impossible de dire qui est en mouvement et qui est au repos.
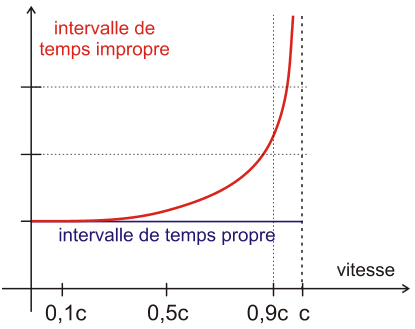
Remarque 3: Pour les faibles vitesses (inférieures à 10% de la vitesse de la lumière), il n'y a pratiquement pas de différence entre les indications des horloges en mouvement et de celles au repos. En revanche, pour les vitesses approchant la vitesse de la lumière, le temps doit être considéré comme une grandeur relative, dépendant de l'observateur qui le mesure.
Ci-dessous quelques exemples chiffrés:
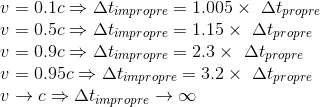
[1] En toute rigueur, l'expérience du pendule de Foucault a montré que la Terre n'est pas un référentiel inertiel, elle est elle-même en rotation par rapport à un référentiel inertiel. Cf Inertial Frame of Reference