Suppose that an observer is standing on the surface of Earth and is pointing a torch in the sky. A pair of events might be the successive peaks of the light wave leaving the torch.

as it moves upwards against a gravitational field
From our article Generalisation of the metric tensor in pseudo-Riemannian manifold, we know that in the non inertial Earth's referential frame, the space time line element between the two events can be written as:
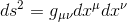
where the indices μ and ν run over 0, 1 ,2, 3 for spacetime.
But as the observer is at rest in his own referential, the only non null coordinates is x0, so that the square of the line element can be simplified to:
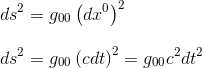
If our observer is at rest in his own referential, we know also how to express the space time distance with respect to the proper time τ (tau), as explained in Proper time article
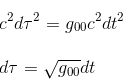
But we know from our previous article The Geodesic equation in the Newtonian Limit that at the surface of the Earth, the metric tensor can be expanded in terms of the gravitational potential as follows
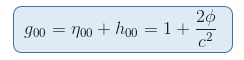
which gives then, by expliciting the value of the Newtonian gravitational potential field at a point in a gravitational field
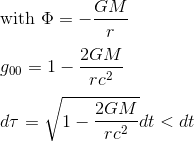
In the above equation, the infinitesimal intervall dt can be considered as the time interval observed in a referential without gravitational effect, or say in another way in a ideal referential situated at an infinite distance
We can therefore write:
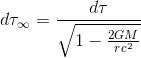
where dτ∞ refers to the period of the light wave as measured by a distant observer without gravity and where dτ is the period of the wave measured where it is emitted, ie from the surface of the Earth.
This equation tells us that clocks run slower in a gravitationnal field as seen by a distant observer, this effect is known as gravitationnal time dilation.
As a direct consequence, because frequency is the reciprocal of the period, we can say:
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.

