Newtonian gravity consists of two equations: one tells us how matter responds to gravity, and the other tells us how matter produces gravity.
The first equation, derived from Newton's second law of motion, says

where a vector is the acceleration through space, nambla is the Euclidean gradient operator and Φ is the gravitational potential.
In this article, we will focus on this first equation, and we will try to derive an approximation of the Newtonian gravitational equation with the mathematics of general relativity.
In the Newtonian limit, we make three assumptions:
- The particle is moving relatively slowly (compared to the speed of light).
- The gravitational field is weak.
- The field does not change with time, ie it is static.
As the geodesic equation describes the worldline of a particle acted only upon only by gravity, our goal is therefore to show that in the context of the Newtonian limit, the geodesic equation reduces to the first Newton's gravity equation, as expressed above.
We recall from our previous article Geodesic equation and Christoffel symbols that the geodesic equation, using proper time as the parameter of the worldline is:
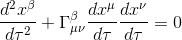
The second term hides a sum in μ and ν over all indices (16 terms). But because the particle in question is moving slowly (first assumption of the Newtonian limit), the time-component (ie the 0th component of the particle's vector) dominates the other (spatial) components, and every term containing one or two spatial four-velocity components will be then dwarfed by the term containing two time components.
We can therefore take the approximation:
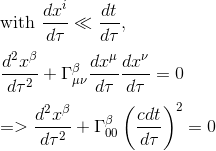
If we restrict ourselves to the Newtonian 3-D space, meaning that we assign β to spatial dimensions only, we can then replace β by the latin letter i (i = x, y, z), giving:
Equation 1
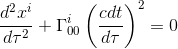
From our article Christoffel symbols in terms of the metric tensor, we know how to calculate the Christoffel symbol with respect to the components of a given metric:
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.

