Welcome to Einstein Relatively Easy!

This web site is aimed at the general reader who is keen to discover Einstein's theories of special and general relativity, and who may also like to tackle the essential underlying mathematics.
Einstein's Relativity is too beautiful and too engaging to be restricted to the professionals!
Have fun!
"I have no special talents
I am only passionately curious"
Albert Einstein
Geodesics from covariant derivative
- Details
- Category: General Relativity
- Hits: 11931
A geodesic of spacetime is a curve that is straight and uniformly parametrized, as measured in each local Lorentz frame along its way.
If the geosidesic is timelike, then it is a possible wordline for a freely falling particle, and its uniformly ticking parameter λ (called affine parameter) is a multiple of the particule's proper time, λ = κτ + μ.
This definition of geodesic translates into the abstract and coordinate-free language: a geodesic is a curve P(λ) that parallel-transports its tangent vector u = dP/dλ along itself.
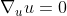
Now defining a coordinate system {xα(P)), along with basis vectors eα = ∂/ ∂xα, we can define the tangent vector u and its components
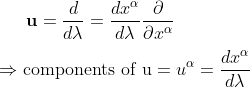
and thus finally the component version of the abstract geodesic equation definition becomes

CQFD
This geodesic equation can be solved (in principle) when both initial data xα and dxα / dλ have been specified.
Advance of the perihelion of Mercury
- Details
- Category: General Relativity
- Hits: 12904
Another test that Einstein suggested for testing his gravitational theory was the precession of perihelia. This reflects the fact that noncircular orbits in General Relativity are not perfect closed ellipses; to a good approximation they are ellipses that precess.
The strategy is like as in our previous article about light deflection to describe the evolution of the radial coordinate r as a function of the angular coordinate Φ; for a perfect ellipse, r(Φ) would be periodic with period 2π, reflecting the fact that perihelion occured at the same angluar position each orbit.
Using then perturbation theory, we can show how General Relativity introduces a slight alteration of the period, giving rise to precession.
We recall from our previous article Gravitational deflection of light the relativistic expression of the Binet's equation (in Newtonian physics, the last term in u2 is absent) for a particule with mass (note the presence of the term GM/h2 on the right-side of the equation)
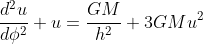
If we now consider a circular orbit with constant radius rc: rc should be solution of the previous equation so that, with uc=1/rc:
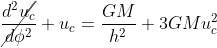
If we now assume that the solution has the form