Another test that Einstein suggested for testing his gravitational theory was the precession of perihelia. This reflects the fact that noncircular orbits in General Relativity are not perfect closed ellipses; to a good approximation they are ellipses that precess.
The strategy is like as in our previous article about light deflection to describe the evolution of the radial coordinate r as a function of the angular coordinate Φ; for a perfect ellipse, r(Φ) would be periodic with period 2π, reflecting the fact that perihelion occured at the same angluar position each orbit.
Using then perturbation theory, we can show how General Relativity introduces a slight alteration of the period, giving rise to precession.
We recall from our previous article Gravitational deflection of light the relativistic expression of the Binet's equation (in Newtonian physics, the last term in u2 is absent) for a particule with mass (note the presence of the term GM/h2 on the right-side of the equation)
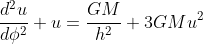
If we now consider a circular orbit with constant radius rc: rc should be solution of the previous equation so that, with uc=1/rc:
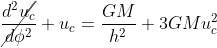
If we now assume that the solution has the form
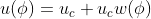
and subsituting in the above equation, we find
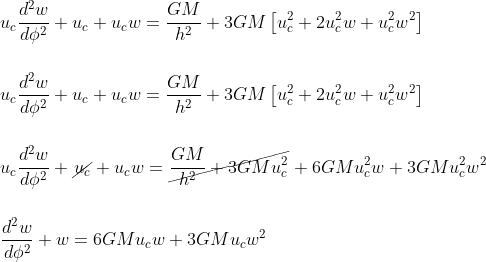
Adding now the hypothesis that w<< 1, we get
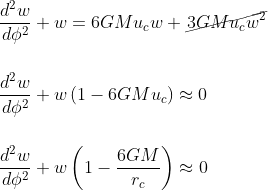
This equation looks like the equation of the harmonic oscillator d2x/dt2 + ω2x = 0 where 1-6GM/rc = ω2.
We know that the solution to this equation can be written as x(t) = A cos(ωt + t0) where A and t0 are constants, thus the solution to our equation looks like
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.
The correct value is in fact just the precedent value of 41.11'' which sould be corrected by (1-e2)
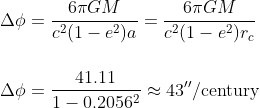
Einstein triumphantly announced this result in the third of his four November lectures.
"This discover was, i believe, by far the strongest emotional experiment in Einstein's scientific life, perhaps in all his life," Abraham Pais later said. He was so thrilled he had heart palpitations, as if "something had snapped" inside.
Remark: the observed value of Mercury's orbit precession is 5601 arcsecs/100 years. However, much of that (5025 to be precise) is due to the precession of equinoxes in our geodesic coordinate system; the gravitational perturbations of the other planets contribute an additional 532 arcssecs/100 years, leaving 43 arcsecs/100 years to be explained by General Relativity.
Which it does quite well ;-)

