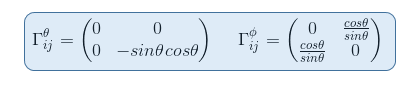In this article, our aim is to calculate the Christoffel symbols for a two-dimensional surface of a sphere in polar coordinates.
We have already calculated some Christoffel symbols in Christoffel symbol exercise: calculation in polar coordinates part I, but with the Christoffel symbol defined as the product of coordinate derivatives, and for a two dimensional Euclidian plan.
Here we will be using the formulation relative to the metric found in the previous article Christoffel symbols in terms of the metric tensor and we will apply it for the surface of a sphere.
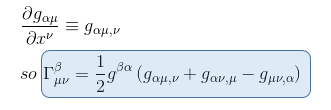
From the previous article Metric tensor exercise: calculation for the surface of a sphere, we know that the metric and the inverse metric describing the surface a sphere are respectively
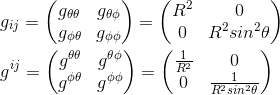
In polar coordinates, we know that we have to find the eight following symbols:

Let's start by calculating the four symbols with θ as upper indice. We can write:
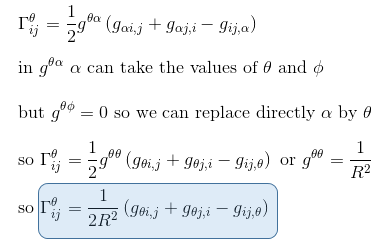
The four first symbols are now very easy to deduce:
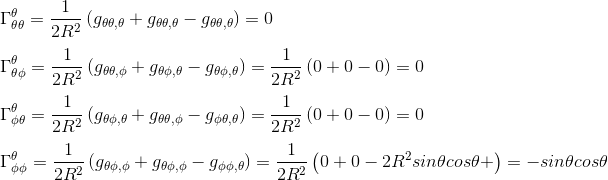
These four values could be summarized in our first matrix:
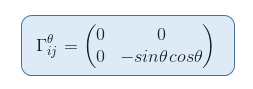
It's now time for us to calculate the four symbols with φ as upper indice. We can write:
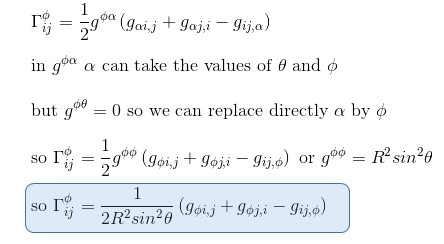
From there, we can easily deduce the last four connection coefficients:

So finally for a surface of a sphere, the eight Christoffel symbols are equal to: