In this section, as an exercise, we will calculate the Christoffel symbols using polar coordinates for a two-dimensional Euclidean plan.
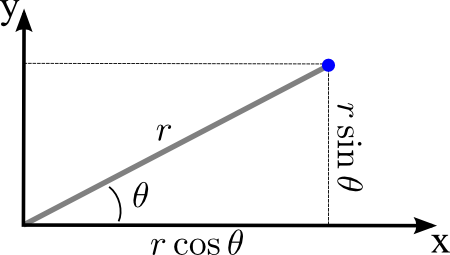
and given the fact that, as stated in Geodesic equation and Christoffel symbols
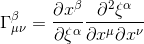
we are then ready to calculate the Christoffel symbols in polar coordinates. As we know from the definition of Christoffel Symbol or Connection coefficient, in 2 dimensional space, we have to find 2x2x2 = 8 connection coefficients, and only 6 distinct values because of the symmetry on the lower indices.
The eight Christoffel symbols to find are summarized in the two matrix below, with the symbols being symmetric on the lower index (meaning that the connection coefficients that are linked below by the blue arrow are equal).
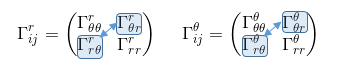
Let's start by populating the four values of the first matrix with r as upper indice:

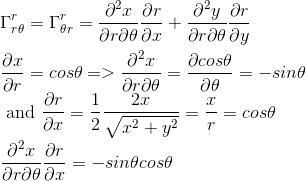
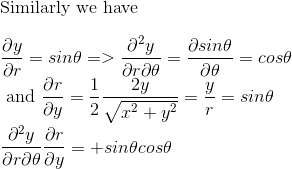
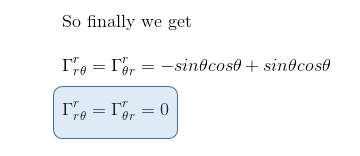

This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.

