
In the same way as we have generalized the formulation of a geodesic equation from an inertial referential to an arbitrary referential (see Geodesic equation and Christoffel symbols), our first goal in this article is to generalize the definition of the metric tensor from a Minkowski spacetime (see The Minkowski metric) to the one of a so called pseudo-Riemannian manifold, which is the mathematical structure by which the General Relativity spacetime can be modelled.
Generalization of the definition of the metric tensor
If we adopt the same convention as in the article Geodesic equation and Christoffel symbols, by naming the spacetime coordinates ξα in the local inertial referential, i.e: ξ0 = ct, ξ1 = x, ξ2 = y, ξ3 = z, we can then write the Minkowski line element as follows
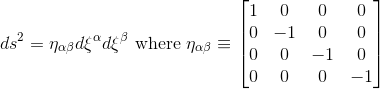
Let's name xμ the coordinates in the new arbitrary referential (non inertial), we can then write given that
ξα = ξα(x0, x1, x2, x3) , and so that an infinitesimal variation dξα is:

The metric tensor has also the following properties:
- - it is symmetric in the sense of gμν = gνμ (the entries of a symmetric matrix are symmetric with respect to the main diagonal)
- - the inverse matrix is noted gμν[1] and is defined as folllows in absract notation: gμαgαν = δμν (Kronecker delta)
The metric tensor gμν is of fundamental importance: it contains all the information of the spacetime and because spacetime curvature is equivalent to gravitation, the metric contains all the information about the gravitationnal field. The goal of the general relativity could be therefore defined as to be able to calculate this metric. For symmetry reason, it is easy to see that the 16 metric components can be reduced to only 10 independant values.
To get familiar with this metric formulation, we will dedicate the next article Metric tensor exercise: calculation for the surface of a sphere to the calculation of the metric of the surface of a sphere of a radius R in polar coordinates.
[1] There is a precise reason why the inverse metric is noted with upper index: as we will see later in our article dedicated to the Introduction to Tensors, it is a rank-2 contravariant tensor, whereas the metric tensor itself, which is a rank-2 covariant tensor, is noted with lower indexes.

