The definition of a manifold captures the idea that the coordinate systems are local, and constraints the permitted transformations between these local coordinates. In this sense, a surface is a two-dimensional manifold; space-time is a four-dimensional manifold.
The Metric tensor g allows one to define and compute the infinitesimal distance on the manifold:
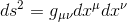
We recall that the physical significance of this is that if we have a small displacement in spacetime (dt, dx, dy, dz) then ds is the total distance moved, and also that this quantity is an invariant, i.e all observers in any frame of reference will agree on it.
A metric is positive definite if ds2 is always positive, and Riemannian manifolds have a metric that is positive definite.
Special Relativity
We know that in Einstein's Special Relativity, the space-time interval is given by the following specific form, as derived from our article The Minkowski metric

where ημν is the Minkowski metric tensor.
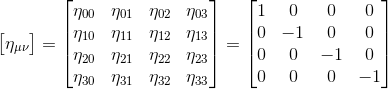
We recall also that as explained in Minkowski Space-Time, depending on the values of dt, dx, dy, dz the spacetime separation ds2 may be positive, negative or zero, which correspond to timelike, lightlike and spacelike intervals respectively. Therefore, the Minkowski spacetime is NOT a Riemannian manifold.
We call the signature (p,q,r) of the metric tensor g the number (counted with multiplicity) of positive, negative and zero components of the metric tensor.
We call a Lorentzian manifold a manifold in which the metric signature is (1, N−1) for a N dimensional space.
Given the fact that the signature of a diagonal matrix is the number of positive, negative and zero numbers on its main diagonal, the Minkowski metric has a signature (1,3) in four-dimensional spacetime, and therefore Minkowski spacetime is a special case of Lorentzian manifold.
General Relativity
Now, what can we say about the curved spacetime in General Relativity?
In General Relativity, as derived from our article Generalisation of the metric tensor in pseudo-Riemannian manifold the metric is:
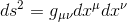
In this context also ds2 could be positive, null or negative, and the earlier discussed notions of time-like, light-like and space-like intervals in special relativity can similarly be used to classify one-dimensional curves through curved spacetime. A time-like curve can be understood as one where the interval between any two infinitesimally close events on the curve is time-like, and likewise for light-like and space-like curves. Technically the three types of curves are usually defined in terms of whether the tangent vector at each point on the curve is time-like, light-like or space-like.
As this metric could be negative but of the form (-,-,+,+) so with a signature (2,2) and not (1,3) it is NOT considered as a Lorentzian metric and as it is NOT positive definite (ds2 >0), it can NOT be a Riemaniann metric tensor neither.
The metric which determines the curved spacetime of General Relativy is a pseudo-Riemannian metric, attached to a so called pseudo-Riemannian manifold.
Remark: a Lorentzian manifold in which the signature of the metric is (1, n−1) (equivalently, (n−1, 1) is a special case of a pseudo-Riemannian manifold but obviously the inverse is not true.

