As suggested by Richard P. Feynman in his lecture dedicated to Special Relativity, we should look at the Lorentz transformations in the same way as what is happening for an 'ordinary' object: when we look at an object, its depth and width are only apparent and will be different if we step aside and look at the same object from a different optical angle.
By analogy, we should think about space and time coordinates as only 'apparent' properties depending on our velocity; in other words, in the space measurements of one man there is mixed in a little bit of the time, as seen by the other and vice versa. We don't easily get this intuition because as we have had no effective experience of going nearly as fast as light in the past, our brain is unable to apprehend the fundamental unique nature of the concepts of space and time, and to recombine them together as it would do for width and length when we move around an object to a new position.
This new kind of world where events occupying space and lasting for a certain length of time [1] could be viewed from different points of view when we are moving at different (high) velocities is called space-time or spacetime. The spacetime itself can be viewed as the union of all events.
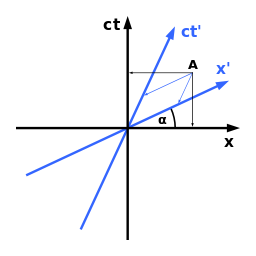
flat Minkowski spacetime
Spacetime is independent of any observer. However, in describing physical phenomena, each observer chooses a convenient metrical coordinate system. By example, in our article The Lorentz transformations Part V - 2nd observer in Minkowski spacetime diagram, we have shown how an observer who is moving has to use a set of axes which are inclined equally to the light ray, with an angle of tanα = c/v, v being the speed of the moving observer.
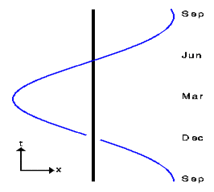
The world line of a particle or light beam is the path that this particle or beam takes in the spacetime and represents the history of the particle or beam. The world line of the orbit of the Earth (in such a description) is depicted in two spatial dimensions x and y (the plane of the Earth's orbit) and a time dimension orthogonal to x and y. The orbit of the Earth is an ellipse in space alone, but its world line is a helix in spacetime.
The Minkowski metric determines the geometry of the spacetime of the same name, as well as determining the geodesics of particles and light beams.
As we know, this metric plays a fundamental role in the expression of spacetime interval
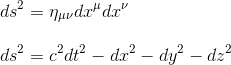
Depending on the values of ct,x,y,z the spacetime separation ds2 may be positive, negative or zero.
Below are the three ways that an event E at the origin may be related to other events in spacetime
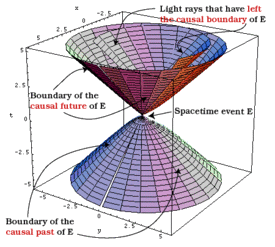
- Time-like interval: where ds2 > 0, describes events within E's lightcone. These events are causally related to E, anf there will be some inertial frame where E and the other event from the interval occur at the same place but at different times.
- Space-like interval: where ds2 < 0, describes events outside E's lightcone. These events are NOT causally related to E, anf there will be some inertial frame where E and the other event from the interval occur at the same time but at different places.
- Light-like interval: where ds2 = 0, describes events on E's lightcone. These events are causally related to E, but they can only be linked to E by a light signal.
Remark: we have also come across this classification in our article dedicated to Four-velocity vector inner product
[1] These events could be then considered as a kind of 'blobs' of a mixture of space and time

