In our previous article Minkowski spacetime and time dilation calculation, we have explained how to visualise the time dilation effect among two inertial referentials Ziga and Ranja in constant velocity v relative to each other via the Minkowski space time diagram.
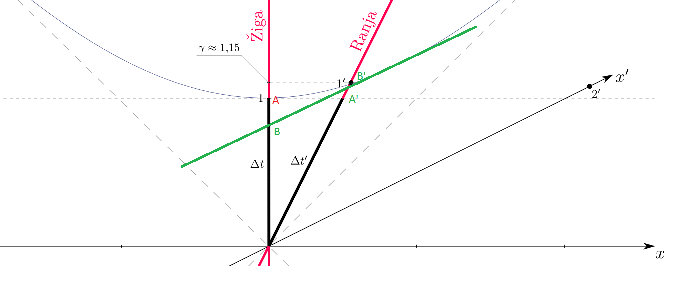
However, we did not really explain how to show the second inertial frame Ranja belonging to a second observer O'. How do we draw the ct' and x' axis relative to Ranja referential?
Each possible event that can happen in frame Ranja when the spatial coordinate x' equals zero, joined together, will form the ct' axis. So we just have to consider the point x'=0 : this point is moving along the x axis with a velocity v (as the frame Ranja is moving at this velocity)
We could state that if an object is travelling with a constant velocity v then that velocity will equal distance travelled divided by time taken and is given by
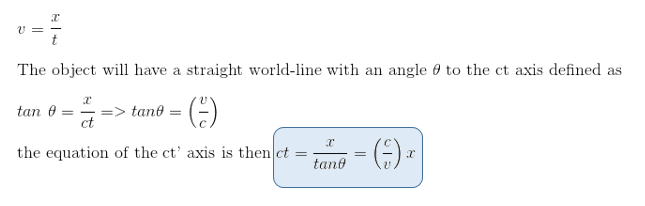
But we could have found this equation directly using the Lorentz transformations:
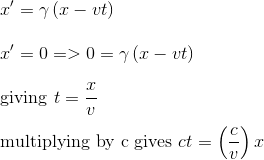
Similarly, if we want to find the equation of the x' axis, which is the line where ct'=0, we deduce from Lorentz transformation applied to ct' transformation:
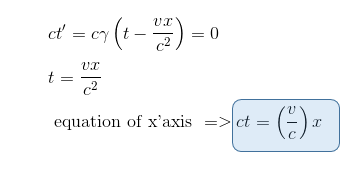
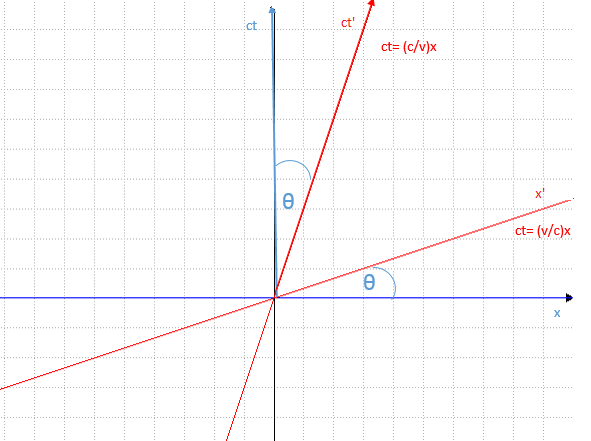
The figure belows shows the lines ct = (v/c) x and ct = (c/v) x, which are the equations of the x' and ct' axes of a frame R' moving with speed v relative to S.
The angles between ct' and ct and x' and x are equal and are defined as tan θ = v/c.