In our previous articles, we have seen that the time dilation factor, also known as the Lorentz factor γ, becomes measurably larger than 1 only for objects or referentials that can move close to the speed of light.
Ideally, we would like to find an object with a given lifetime and we could then look to see if we could prolonge his lifetime simply by moving it fast.
The muon particle[1] meets these requirements as it has a very short lifetime: it decays via the weak interaction into an electron and in another pair of subatomic particles called neutrinos after 2.2 microseconds. Also, because this particule is very small, it very easy to be accelerated to very high speeds.
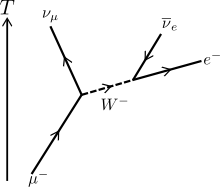
In the late 1990s, scientists at Brookhaven National Laboratory on Long Island, New York, used the Alternative Gradient Synchrotron (AGS) to produce beams of muons circulating around a 14-meter-diameter ring at a speed of 99.94 percent of the speed of light.
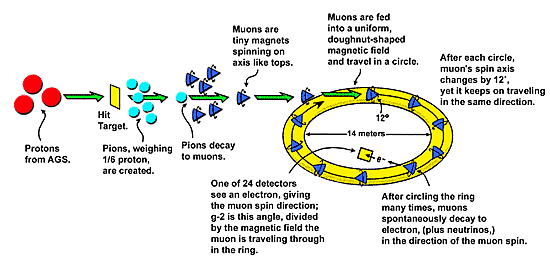
If muons live for only 2.2 microseconds at this speed, then they would manage no more than 15 laps of the ring before they died.
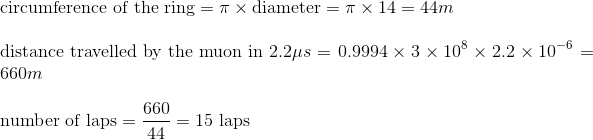
In reality they managed around 433 laps, which means their lifetime extended by a factor of 28.8 to just over 60 microseconds.
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.
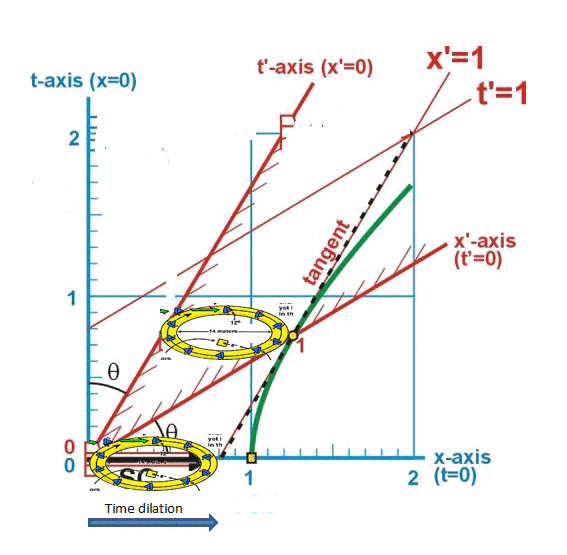
.
[1]The muon is an elementary particle similar to the electron, whith electric charge of -1 and a spin of 1/2, but with a much greater mass. It is classified as a lepton, along with the electron, the tau and the three neutrinos.

