Another common way of expressing the Lorentz transformation is in matrix form:

Recalling the rules for matrix multiplication we see that:
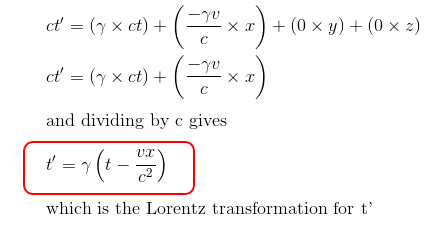

We have found exacly the same Lorentz transformation equations as described in The Lorentz transformations Part I - Presentation
The two ways of expressing the equations are strictly equivalent.
We can write an even more compact form by using the index notation (see tab Index Notation)
We can write the Lorentz matrix in a even more compact notation, using index notation, in the form:

where the indices μ and ν take the values of the number of spacetime dimensions, ie 0 to 3.
So the components of x'μ are (x'0, x'1, x'2, x'3) = (ct', x', y', z')
And those of xμ are (x0, x1, x2, x3) = (ct, x, y, z)
Concerning the matrix,
the μ index refers to the μth row and the ν index refers to the νth column



