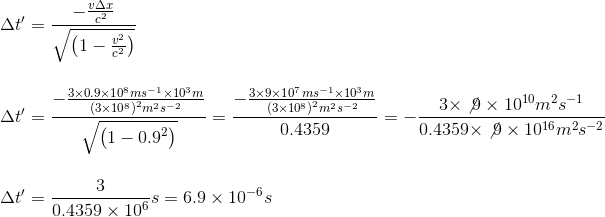Note: The consequences of the Lorentz transformations regarding the behaviour of clocks and measuring as it will be exposed in this article are described by Einstein in Chapter 12 of his book Relativity.
We are mentionning here two supplementary consequences which are the spacetime invariance and the conservation of the light speed in different inertial frames.
You can find a synthetic demonstration of all these effects in the following contribution also: Thread about Lorentz transformation
Length contraction
Suppose a metre-rod in the x' axis of R' in such a manner that one end (the beginning) coincides with the point x'=0 whilst the other end (the end of the rod) coincides with the point x'=1. What is the length of the metre-rod relatively to the system R?
As we know, we just have to take a photography from the rod in our R referentiel at a given time. Let's choose t=0, as we are now used to.
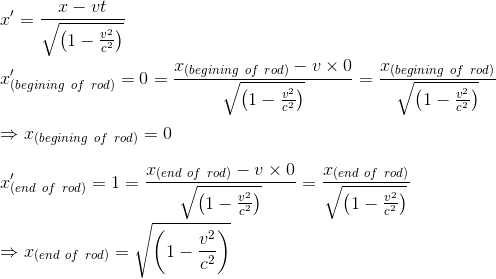

But the metre-rod is moving with the velocity v relative to R, so the rigid rod is thus shorter when in motion than when at rest, and the more quickly it is moving, the shorter is the rod.
For the velocity v=c we should have 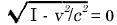 ,
,
and for still greater velocities the square-root becomes imaginary. From this we conclude that in the theory of relativity the velocity c plays the part of a limiting velocity, which can neither be reached nor exceeded by any real body.
For illustration purposes, let's suppose that a referentiel R' is moving with a relative speed of 0.6 times the speed of light with reference to frame R; it is now very easy to calculate by how much the rod is then shortened from R frame's point of view
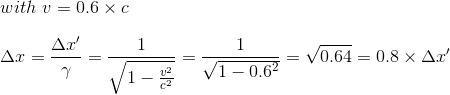
Time dilation
Let us consider a seconds-clock which is permanently situated at the origin x'=0 of K'.
t'=0 and t'=1 are two successive ticks of this clock.
The first and fourth equations of the Lorentz transformation give for these two ticks :
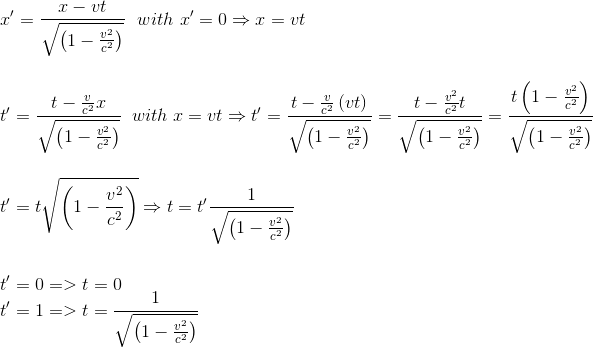
As judged from R, the clock is moving with the velocity v; as judged from this reference-body, the time which elapses between two strokes of the clock is not one second, but γ > 1.
As a consequence of its motion the clock goes more slowly than when at rest.
Remark: we confirm here that the time dilation γ found by the Lorentz transformation is the same that we did find geometrically in our introduction article about time dilation Constant Speed of light - Introduction to Time Dilation and Lorentz factor
As we have earlier calculated the length contraction observed by a moving referential animated with a speed of 0.6 speed of light, let's try to calculate the time dilation observed from the 'fixed' R referential
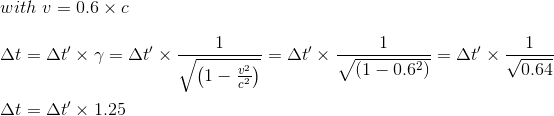
Speed of light invariance
To check the correctness of Lorentz transformations, we should make sure that the second postulate of special relativity, i.e the speed of light remains equal in all inertial referentials, holds true.
If a light-signal is sent along the positive x-axis of the frame reference R, its motion will obey the equation
x = ct with c defined as the speed of light
According to the equations of the Lorentz transformation, this simple relation between x and t implies a relation between x' and t'.
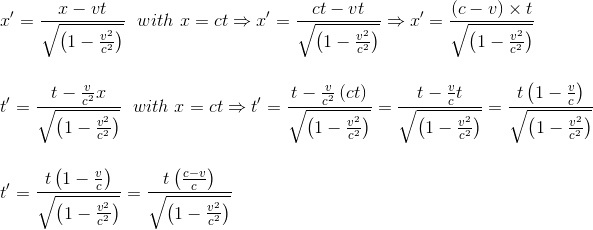
Calculating the speed of light in R' referential is now straightforward
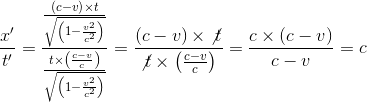
We just have verfied that the speed of light remains constant between two referential frames transformed by Lorentz equations.
End of simultaneity
We have seen in one of our first articles that the simultaneity of events could depend on the observer's reference frame.
This can be now shown algebraically using the interval transformation rule
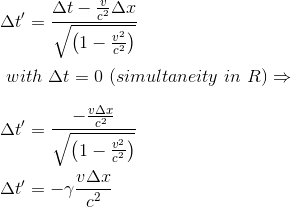
Remark 1: The interval of time will expand as the relative speed or/and the distance is increasing.
Remark 2: Inversely, for very low speeds where v << c, then the time interval tends to 0.
As an exercice, let's try now to calculate the inteval of time observed by the cosmonaut between the lauching of the two rockets, as seen in our article Constant Speed of light - Introduction to End of Simultaneity

Suppose that the cosmonaut travels at the speed of 0.9 speed of light (noted c) and that the two rockets are separated by a distance of 1km = 103m.