When Einstein first hit upon special relativity, he thought one effect had special importance, so much so that it fills the first section of his "On the Electrodynamics of Moving Bodies." It is the relativity of simultaneity - see Kinematical Part - Definition of simultaneity.
According to it, inertial observers in relative motion would disagree on the timing of events at different places.
Let's try to illustrate this by the following scenario, first in classical Newtonian (non relativistic) context.
In Newtonian Context
In the exact middle of a train coach, a speaker has been set up to emit at time t=t'=0 a sound wave travelling with speed v towards each part of the coach.
Suppose that a referentiel R is attached to the ground, with the origin O located at time t=0 at the middle of the coach, i.e. at the place of the speaker.
Suppose also that a referentiel R' is attached to the coach in a standard configuration, which means:
- The x, y axes of frame R are parallel to the x', y' axes of frame R'.
- The origin of frame R' is moving with velocity u as measured relative to R.
- The origin of frames R and R' coincide when time t=0 in frame R and when time t'=0 in frame R'.
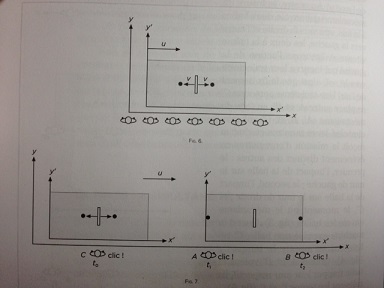
Train at rest u=0
If the train is at rest in frame R, i.e the velocity u=0, and if L is the length of the coach, we deduce immediately that the time Ta when the observer in R is hearing the sound on the left side of the coach and the time Tb when the observer in R is hearing the sound reaching the right side B of the coach are given by:
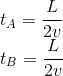
Train in uniform movement with u> 0
We suppose now that the train is moving towards the right at a constant speed u relatively to the observer on the platform.
The time Tb at which the observer on the platform will hear the sound reaching point B of the coach is given by the following equation:
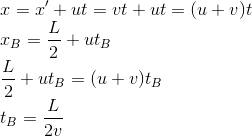
Let's try to calculate now the time ta at which the observer on the platform will hear the sound reaching the left coach

In both situations, the train at rest or in movement, the observer in the fixed referential will hear the sound hitting both sides of the coach at exactly the same time.
Left sound has less distance to travel to reach point A as the coach moves against it, but it is compensated by a lower speed u-v, as heard from the platform.
Inversely, right sound has more to travel as the coach moves away from it, but it's cancelled by his faster speed u+v, as heard from the platform.
In Relativistic Context
On an orbital station, it has been agreed that two rockets should take off exactly at the time when they would both receive a light signal emitted by a control tower located at the same distance from each other.

Inertial frame of reference = Surface of the planet
As the light travels the same distance at the same speed, the light would reach the two rockets simultaneously, and the observer watching this scene from the ground would see the two rockets taking off exactly at the same time, as expected.

Inertial frame of reference = Spaceship travelling at constant high speed v to the right
Now suppose that we choose as a new referential frame an observer piloting a spaceship travelling with a very high and constant speed to the right.
The cosmonaut will still see the two light signals leaving the tower of control exactly at the same time (two events happening at the same time at the same place in an inertial frame of reference will always been seen as simultaneous in any other frame of reference).

But as the spaceship is travelling to the right side, the planet and the orbital station are relatively shifting to the left side. If it's the case, then the right rocket is moving towards the spaceship whereas the left rocket is moving away from it.
The right ray of light will then have less distance to travel to reach the right rocket, and recalling the second postulate of Special Relativity that the speed of light is constant in any inertial frame, the right light ray would then reach the right rocket first.

Then only a tiny bit later (we will in an another course that this time interval will both depend on the speed of the spaceship and on the distance L between the two rockets) that the pilot will see the left ray of light hitting the left rocket.
Therefore, from the spaceship point of view, the takeoff of the two rockets is not simultaneous.

This shows that events that appear simultaneous in one reference frame, may not do in another, and that what we perceive as the present only corresponds to what is occurring simultaneously to us, in our reference frame.

