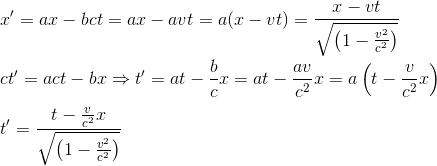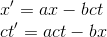Note: the simple derivation of the Lorentz transformation as it will be exposed in this article is done by Einstein in Appendix 1 of his book Relativity. We are giving here a little bit more detailed calculus.
Again with take the hypothesis of two referentials R and R' in standard configuration.
We require to find x' and t' when x and t are given, assuming that R' is moving along the x axis relative to R.
A light-signal, which is proceeding along the positive axis of x of the referential R, is transmitted according to the equation
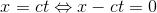
Likewise, since the same light-signal has to be transmitted relative to R' with the same velocity c, the propagation relative to the system R' will be represented by the analogous formula
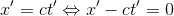
The only way that the same event could satisfy the two equations is if
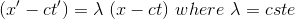(1)
so that at t = t' = 0, the disappearance of (x - ct) involves the disappearance of (x' - ct')
If now we apply quite similar considerations to light rays which are being transmitted along the negative x-axis, we obtain the equivalent formula
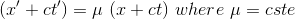(2)
If we now sum up equations (1) and (2) we get:
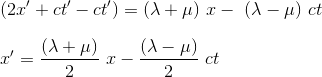
Substracting (2 and (1) gives the equation of ct'
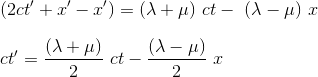
By defining a and b as follows
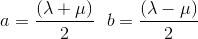
we can rewrite the two equations simply like
|
|
Our problem becomes now to find a and b.
If we try to find the the movement of the origin of R', given by x'=0, with the reference to R, we just have to use first equation
We can now express the speed of the referential R' with a,b and c = speed of light.
If now we were to express the length of a solid stick measuring 1m in referential R', from the referential R, we just have to take a photography of this stick at a given time, say at t=0 in R. Using the first equation, we get
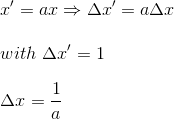(equation 3)
Let's do the same exercise from the R' perspective; we need to take a snapshot of the stick at a given time t' in the R' referential. We guess that we have to choose t'=0
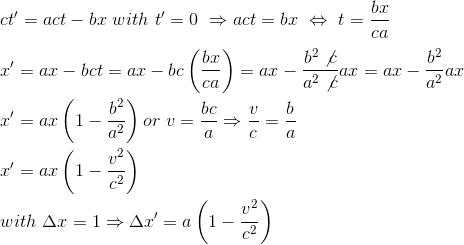
(equation 4)
But we know that the stick length in R' seen from R should be equals to its length in R observed from R', hence equation 3 = equation 4
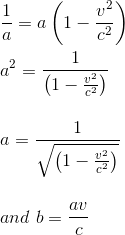
we can then rewrite our two main equations expressing x' and t', and verify that they conform to the Lorentz expression as given in the precedent article The Lorentz transformations Part I - Presentation
