
As per the considerations of the Equivalence Principle, if we were to describe the movement of an object in the Earth's gravitational field, we would then have to follow the following steps:
- Describe the movement in a local inertial free falling referential
- Operate a coordinate transformation from this local inertial referential to the Earth referential, this one seen as accelerated upwards
Step 1: Describe the movement in a free falling referential
Note: You can refer to this article The Lorentz transformations Part IV - Lorentz transformation matrix (tab index notation) for a gentle introduction to the index notation and Einstein summation convention if you are not familiar with these concepts.
In the free falling referential, let's name the spacetime coordinates ξα in index notation, i.e:
- α ∈ {0,1,2,3}
- and ξ0 = ct, ξ1 = x, ξ2 = y, ξ3 = z
The movement of the free particule is given by the four-acceleration vector's magnitude equal to 0 so using the index notation:

With τ refers to the time as measured by an observer at rest in his own rest referential also called the Proper time for a non massless particle.
Step 2: Describe the movement in Earth referential (accelerated towards the upper direction)
Let's name xμ the coordinates in the new arbitrary referential (non inertial)
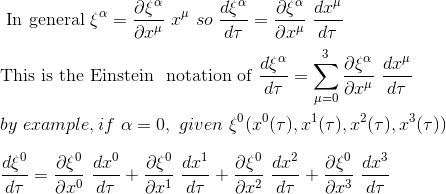
So applying the chain rule to our initial free-falling equation we get:
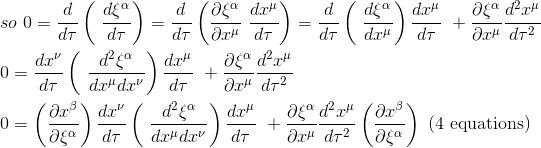
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.

