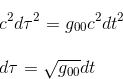The proper time noted by convetion τ (tau) is by definition the time measured by an observer in their own rest frame, i.e the time between two events as measured in a frame where the events stay in the same position.
In the case of a particule, proper time would be then the time given by an imaginary clock strapped to the particle, or a kind of 'internal clock'.
We should think of the signification of 'proper' as a synonym of 'property', not as synonym of 'correct' (in Special Relativity, as we know, there is no 'correct' observer or referential)
Consider Δt as an infinitesimal lifetime interval of a particule measured in its on rest frame, the spacetime interval between any two positions of a particule in such a frame is given by
Δs2 = c2Δt2 - Δx2 - Δy2 - Δz2 = c2Δt2 - 02 - 02 - 02 = c2Δt2
But as propert time Δτ, by definition, is the time measured by an observer in their own rest frame, we can say Δτ = Δt and therefore
Δs2 = c2Δt2 = c2Δτ2
Since the interval is assumed timelike - refer to the article Minkowski Space-Time for the definition, one may take the square root of the above expression
Δs = cΔτ or Δτ = Δs/c
and the proper time interval is defined as
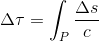 where P is the worldline from some initial event to some final event
where P is the worldline from some initial event to some final event
Also, as the spacetime separation of events is an invariant quantity, ie is measured the same for all inertial observers, the following quantity c2Δτ2 holds same not only for events occuring at the same position, but also applies to time separated events measured from any frame R'
c2Δτ2 = Δs'2 = c2Δt'2 - Δx'2 - Δy'2 - Δz'2
We have demonstrated in our article Minkowski's Four-Dimensional Space-Time (tab time dilation calculation), that this invariance interval gives us the relation between Δτ and Δt. We have found that :
Δτ = (Δt' / γ)
As γ>1, another way of seeing it is that the process that takes a certain proper time (Δτ measured by definition in its own rest frame) has a longer duration Δt' measured by an another observer moving relative to the rest frame, ie moving clocks run slow.
To summarize,
|
c2Δτ2 = Δs2 is an invariant quantity in Minkowski spacetime (which is equivalent to say that it remains the same by Lorentz transformation) => For two inertial referentials in uniform rectilinear motion with respect to each other, the proper time will be the same ( the proper clocks get older at the same pace)[1], whereas the coordinate time observed from each other will run slow. |
You can refer to the article Length contraction use case - Destination Andromeda! for an example of proper time dilation calculation.
[1] This is no more true when one referential is in acceleration relative to the otherl: both proper times are no more equal and this is how we resolve the famous Twin paradox.
In General Relativity, as we have shown in the article Gravitational redshift or Einstein effect - Part I, infinitesimal proper time dτ is defined as follows (by replacing ημν from the special relativity with the general metric tensor gμν)
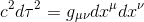
In the same way that coordinates can be chosen such that x1, x2, x3 = const in special relativity, this can be done in general relativity too. Then, in these coordinates