|
What to remember from this article
Minkowski spacetime is the most common mathematical structure on which special relativity is formulated. It has the following features:
|
Minkowski space time diagram
As already explained in our introduction, the special theory of relativity describes the relationship between physical observations made by different inertial or nonaccelarating observers, in the absence of gravity.
Each such observer labels events in space-time by four inertial coordinates t, x, y, z.
In Newtonian mechanics, events are described using a three-dimensional Euclidean space time plus an independant scale of absolute time.
In special relativity (as in general relativity), space and time are fused together into a single four-dimensional entity known as spacetime.
The words of Hermann Minkowski - a german mathematician and also Einstein's professor at Zurich polytechnic - delivered at the 80th Assembly of German Natural Scientists and Physicians (21 September 1908), and by which he introduced spacetime to the world, are now famous:

"The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality."
Although we still use the Cartesian coordinates (x, y, z) as spatial coordinates to specify where the event happened plus a time (t) coordinate describing when it happened, we have to move away from the familiar Euclidean space we have become used to using so far. Let's try to see why.
Consider two events in space time, let's say the start and the end of the famous cyclosportive La Marmotte, covering a distance of 174.4 km (108.4 mi). Let's suppose that it takes you eight hours to finish the race: what does it mean exactly that in the earth's referential your bike computer has measured the exact distance between Bourg d'Oisans and L'Alpe d'Huez to be 174.4km and that you measured the time interval using a clock at Bourg d'Oisans and another - synchronized - one displaying the arrival time in Alpe d'Huez, and found 8h.
Don't forget that we already know that these two distances, both in space and in time, are not universally agreed upon. Someone able to watch your race from a space rocket would say that it did not take you eight hours to finish the race neither that the total distance of La Marmotte is 174.4km.
It's like Einstein has upset the order of things, and that we cannot even rely on both space and time to build a reliable picture of the universe.
It's certainly time to make a conjecture to save the edifice: if the two concepts of time and space are relative to a moving observer, can we not search for some kind of unification of the two which would not vary between two different referentials?
Let's make the radical conjecture that the distance in spacetime is invariant for all observers; let's suppose that distance is a measure that we can all agree upon.
But how do we visualise a distance in a four-dimensionnal spacetime? That's almost impossible, even for Stephen Hawking[1], and we usually reduce our spacetime into a graph of two dimensions, with a vertical time (t) axis and a horizontal spatial (x) axis.
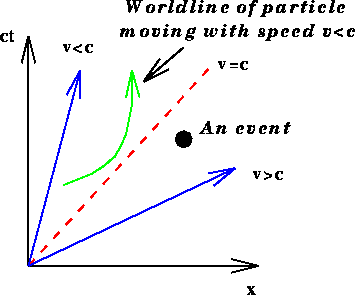
We have also to agree on units, which should be different than the SI ones: given the speed of the light, if we were to choose seconds and meters for our two axes, we would end up with the path of light represented by a line as near as horizontal.
To get around this problem, we multiply the time in seconds by the speed of light in meters per second and use this quantity ct as units for the vertical time axis. One unit of ct is the speed of light (3x108 ms-1) multiplied by the time t ((1/3)x 10-8) that it takes the light to travel 1 meter[2].
Then, by definition, we have defined the speed of light c as being equal to 1m and can now draw the path of a light ray as line with a slope of 45° degrees.
Any particule moving with a lower speed than the light wiill then have a word line steeper than the 45° one, as for a given position on the x axis, it will take it more time to reach it than for the light. Any particule travelling at half speed of the light will have a world line twice as steeper as the light one.
Now let's go back to our initial question to figure out how to calculate the distance in our Minkowski spacetime.
Say that we naively take the formula which holds true in our well known Euclidian space: in our two-dimensional context, we would write this as S2 = x2 + c2t2, which is also the equation of the circle of radius S and center 0.
Put it in other words, for two given events A and O which happened in spacetime, two observers in relative movement to each other could disagree at which position on the x axis and the t axis each event may occur, but if our hypothesis that the spacetime distance remains the same holds true, then we must also accept the contrainst that each event A' (seen by observer 2) or A'' (seen by observer 3) should graphically lie anywhere on the circumference of the circle of radius S.
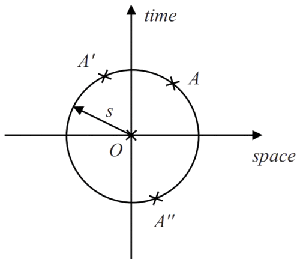
Consider the event A'' : it is on the circle so obviously sits at an equal distance from the event O as the event A.
But there is a big difference: A'' has happened in the past of A, as it sits on the negative part of the time axis.
If we think a little bit on it, something is wrong there: if we consider again our example of the Marmotte race and define the two events 0 and A respectively as the start and the end of the race, we can concede that two observers could see each event at different time and different position, but are we ready to exchange the order of the two events?
If we were to accept this galilean formulation of the distance, it would then mean that it exists somewhere the possibility for an inertial observer to see the arrival of the race before it has even started! The basic causality relation would then be broken, which is quite annoying!
Let's try to see what it would look like to transform the + sign into a - sign, i.e to imagine a spacetime mathematically described by S2 = x2 - c2t2
Pictorially, the locus of points whose squared distance from the origin is ±1 consists of the two hyperbolas labeled +1 and -1 in the figure below:
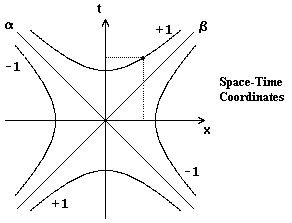
In this spacetime, we can observe that the events siuated at distance +1 of the the origin lie all either on the upper hyperbola (t positive) or either all on the lower hyperbola ( t negative), which marks a real progress compared to our galilean circle.
Minkowski diagram time dilation visualization
Another great feature about Minkowski diagram is that they let us visualize quite easily the time dilation effect between two inertial frames.
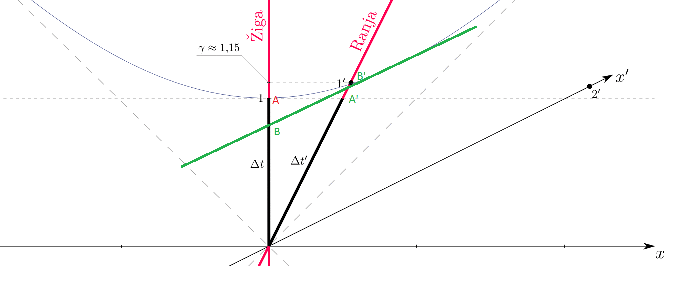
Consider the diagram below with two inertial frames named Ziga and Ranja, with coordinate axis (ct,x) and (ct',x'). We want to find the (coordinate) elapsed time between two events.
Let those two events be the origin and event A (ct=1, x=0) in Ziga referential. To find the coordinate elapsed time in the primed/Ranja coordinate system, draw a line from A, parallel with the x axis - this the line of simultaneity for Ziga for all events happening at ct=1. You then cross the ct' axis of Ranja at the time seen in Ranja referential, here marked as A'. You can clearly see that OA' = Δt' < 1' so from Ranja perspective, time in Ziga (marked as 1 for event A) runs slower.
The Lorentz factor or time dilation factor as experienced from Ziga perspective in the moving referential Ranja can then be visualized as the difference/distance between the projection of A' and B' on the Ziga axis.
The apparently paradoxal proposition, i.e that the time in Ranja runs slower from Ziga perspective, could be visualize exactly in the same way.
Let's define the event B' happening at ct'=1 and x'=0. To find the correspondant event in the unprimed Ziga referential, we have to draw the tangent at this point to the hyperbola: this line defines the line of simultaneity in the primed coordinate system. We have marked this event as B in the diagram below. Again and paradoxally, we can see that OB < 1 in the Ziga referentiel system, which means that from a Ranja observer, the time runs slower in Ziga referential compared to its own referential.
[2] Using ct units of time means we are measuring time in metres.
Minkowski diagram time dilation calculation
In the previous tab, we have seen how the spacetime interval equality ds2 = c2Δt2 - Δx2 - Δy2 - Δz2 lead us to the hyperbola space diagram, where time dilation γ could be graphically represented.
Here we will use the invariance of this spacetime interval for all observers to calculate the exact value of γ. Hopefully we should find the same value as the one found geometrically in the previous article Constant Speed of light - Introduction to Time Dilation and Lorentz factor
Let's suppose that a person Z stands still in Ziga referential sitting down in a train with horizontal speed v relative to Ranja referential.
As Z is at rest in Ziga referential, the values Δx, Δy and Δz are all equal to zero and the spacetime distance that Z has traveled during the time interval Δt in Ziga referential is therefore c2Δt2 - the time as measured by an observer using their own clock is called Proper time.
Now let's consider the same journey from Ranja's perspective. For a person R belonging to Ranja referential, person Z has traveled a distance v×Δt' where Δt' is the time interval Δt as seen from Ranja perspective. So in Ranja referential, person Z has traveled a space time distance ds'2 = c2Δt'2 - Δx'2 = c2Δt'2- (v×Δt')2.
The crucial point here is that both P and Z should agree on the spacetime distance of the journey.
That means that ds2 = ds'2, or also that c2Δt2 = c2Δt'2- (v×Δt')2.
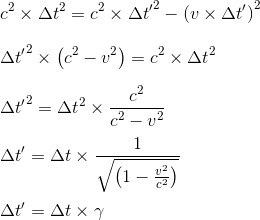
We can check that we have found exactly the same formula for time dilation as the one which emerged by thinking about light clocks in the previous article.

