| "The general theory of relativity must be capable of treating every coordinate system, whatever its state of motion relative to others may be, as "at rest", i.e., the general laws of nature must be expressed by identical equations relative to all other systems, whichever way they are moving." Einsten , Fundamental Ideas and Methods of the Theory of Relativity, Presented in Their Development (1920) |
Covariance:
The term covariance implies a formalism in which the laws of physics maintain the same form under a specified set of transformations.
| Classical Mechanic | Physical laws covariant under Galilean coordinate transformations |
| Special Relativity | Physical laws covariant under Lorentz coordinate transformations |
| General Relativity | Form of physical laws invariant under any arbitrary differentiable coordinate transformation (general covariance) |
Special Relativity
One of the two fundamental postulates of special relativity is the principle of relativity, which stipules that the laws of physics are the same in any inertial frame of reference. Which is equivalent to say that the laws are covariant by Lorentz transformations.
General Relativity
As we know, in presence of a gravitationnal field, the Equivalence Principle allows to formulate all - but gravitationnal - physical laws, in small enough free-falling areas.
To get a macroscopic significant description of these laws, one has therefore to find an operation to link all these different local inertial referentials. That will be to introduce a unique non inertial coordinate system, and that is precisely during this coordinate transformation operation that the effects of gravitationnal field will re-appear.
Indeed we remember from our article Geodesic equation and Christoffel symbols that some kind of 'inertial' forces in case of an accelerated referential or gravitional effect in case of the presence of gravitational field in a rest frame (Equivalence Principle) was now acting in the new arbitrary referential.
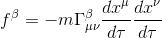
The idea of Einstein was to set the Principle of General Covariance which extends the principle of relativity to say that the form of the laws of physics should be the same in all - inertial and accelerating - frames.
Therefore, to write a valid physical equation in general relativity, we have to write a Tensor equation (which preserves its form under general coordinate transformations) which is true in special relativity, that's all.
By example, the fundamental Newton's first law of motion, is stated as follow in special relativity:
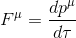
But as the right term is not a tensor - to transform it in a tensor, the usual derivative should be replaced by the Covariant Differentive, so we get the slightly modified Newton's law version in general relativity:
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.

