This article looks at the process of deriving the so called Palatini equation and follows the demonstration found in D'Inverno Introducing Einstein's relativity , Chapter 11-1 (General Relativity from a variational principle, The Palatini equation).
Many tensor identities are derived most easily using the technique of geodesic coordinates in a Local Inertial Frame, where we choose an arbitrary point P at which the Christoffel symbols nullify, which in D'Inverno notation could be written as:
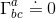
As we know from our article Riemann curvature tensor part III: Symmetries and independant components in this particular case, the Riemann tensor reduces to:
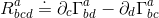
Looking now at a variation of the connection Γabc to a new connection Γabc(hat):
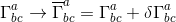
Then δΓ being the difference of two connections, is a tensor of type (1,2), and this variation results in a change in the Riemann tensor between two coordinate systems as:
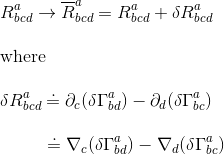
since partial derivatives commute with variation and is equivalent to covariant derivative in geodesic coordinates.
We have now an equation with two tensor quantites on the left hand side (being the difference of two tensors) and on the right-hand side (as by defintion of a covariant derivative). So by definition, if a tensor equatiion holds in one coordinate system it must hold in any coordinate system, we can deduce the Palatini equation - in Inverno notation, it means we can remove the .dot over the equals sign:
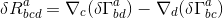
And contraction on indice a and c gives the useful result:
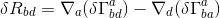
Remark: this last result is used during the process of the Einstein's equation derivation from a variational approach Einstein-Hilbert action

