An alternative route to Einstein's equation is through the principle of least action, as we did previously to deduce the geodesic equation in curved spacetime in Geodesic equation from the principle of least action.
In this article, we will therfore go through the process of deriving the Einstein equations in vacuum and then in the presence of matter using the variational approach.
Action in vacuum
The derivation of the action from a set of equations of motion is very hard, not always possible, and there is no systematic way to do it. We therefore will begin by guessing the action and show that it gives the right answer.
So we will first seek an action S for gravitation that leads to the field equations of general relativity in the absence of matter and energy (in vacuum), that is, we will guess something like:
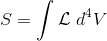
where L is a scalar Lagrange density and d4V is the element of 4-volume. We thus need both a scalar and the 4-volume element.
The 4-volume element is easiest: we recall that in a locally Minkowskian coordinate system xα', the volume element is d4V=dx0'dx1'dx2'dx3'. If there is a positive-determinant Jacobian Jα'β that transforms this to a general coordinate system xβ, we have:
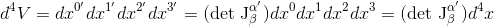
It turns out however that the metric tensor in the general coordinate system is
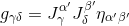
so that if we define g to be the determinant of the 4x4 gγδ matrix, we then have g=-(det J)2, so that if follows that det J = √-g. We thus see that the 4-volume element is
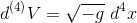
The simplest Lagrangian L that is a scalar function of the metric gαβ and its derivatives is the Ricci scalar R, which can be obtained from the Riemann tensor, as we know from the previous article Bianchi identity and Ricci tensor
Our Lagrangian then is, L=R and we assume that the Einstein-Hilbert action could be epxressed as:
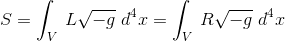
Remark: This integral is taken over the whole of space-time if it converges, and if not, S can still be made so by integrating over an arbitrarily large but compact region; this will still produce the field equations.
You can find an introduction to the Einstein-Hilbert Action at this end of the following Lenoard Susskind's video, starting from 1:11:00 to the end
By its own admission, Susskind has never been able to complete the entire derivation of the Einstein equation from this action, because it's too 'tedious'. Let's see how to do this.
Derivation of the Einstein equation from the Einstein Hilbert action
As we know from the principle of least action, the action variation then requires δS=0
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.
and doing the substitution with k=c4/2(8πG) leads to the familiar Einstein equation which relates the spacetime curvature on the left hand side to the matter energy density on the right hand side
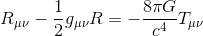
You can follow all the previous demonstration in live in the following excellent youtube tutorial from Robert Davie Variational approach to General Relativity
[1] Introducing Einstein's relativity, Ray D'Inverno, §11.5 Indirect derivation of the field equations.

