This artilce looks at the process of deriving the variation of the metric determinant, which will be useful for deriving the Einstein equations from a variatioanl approach, in the next article Einstein-Hilbert action.
Matrix determinants and trace
Let us consider a matrix from a general form
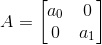
Then the trace of this matrix, as for any square matrix, is the sum of the elements on the main diagonal (the diagonal from the upper left to the lower right), so
Trace(A) = tr(A)=a0 + a1
so that
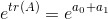
If we now consider the exponential matrix eA as:
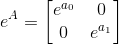
then the determinant of this matrix, defined as the product of the elements on the main diagonal can be expressed as:
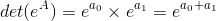
so that finally we can write
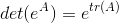
If we now define B = eA

Taking the differential of both sides,
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.
So we finally arrive at the final expression for the variation of the metric, which we will use in the variational approach of General Relativity
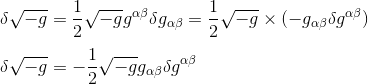
You can watch the live demonstration of the previous result in this excellent video tutorial from Robert Davie

