| "You told us how an almost churchlike atmosphere is pervading your desolate house now. And justifiably so, for unusual divine powers are at work in there." Besso to Einstein, 30 Oct 1915 |
In the last two articles, we have derived the Gμν (Einstein tensor) and Tμν (energy-momenum tensor) components of the Einstein equation:

We have yet to determine the constant k.
To achieve this, we need to show that the Einstein equation reduces to Newton’s law of gravity for weak and static gravitational fields (Newtonian limit).
The first step consists in writing the previous Einstein equation in a slightly different form that is sometimes more practical to use in calculations.
That's actually under this second form that Einstein published it in his article "The Field Equations of Gravitation" submitted on November 25, 1915 in Königlish Preussiche Akademie der Wissenschaften

Einstein's equation alternative form
Replacing Einstein tensor by its full expression:
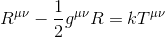
Multiplying both sides by gμν yields to:

By definition of the metric contraction, gμνRμν=R and gμνTμν=T so
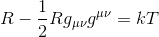
Because the tensor gμν is the inverse of gνα, their product gives the identity matrix of rank 4 = δμα = I (this can be seen by doing the calculation in a local inertial frame where gμν=ημν and noting that since it’s a tensor equation, it’s valid in all coordinate systems). By contracting the δνμ tensor we just sum up its diagonal elements and since these are all one, we get
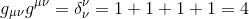
Therefore
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.
We can finally formulate the Einstein equation both in its standard and alternative form
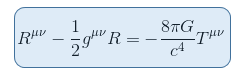

Remark 1: When calculated, the value of K is very very small, meaning that the spacetime is very rigid or stiff: a huge value of mass/energy is required to set a 'noticeable' curvature.

Remark 2: Despite the simple appearance of the equations they are actually quite complicated. Given a specified distribution of matter and energy in the form of a stress–energy tensor, the Einstein Equation or Einstein Field Equations (EFE) are understood to be a set of equations for the metric tensor gμν, as both the Ricci tensor and scalar curvature depend on the metric in a complicated nonlinear manner. In fact, when fully written out, the EFE represent a system of 10 coupled, nonlinear second-order partial differential equations for the metric tensor - corresponding to the 10 independant component of the symmetric tensor gμν.
Remark 3: The non-linearity of the EFE has a profund physical meaning. It relates to the auto-referential role of spacetime in this theory, because it constitutes both the dynamical object and the context within which the dynamics are defined. In other terms, gravitation itself gravites. As stated by Kevin Brown in his Reflections on Relativity, "the self-referential quality of the metric field equations also manifests itself in their non-linearity. Under the laws of general relativity, every form of stress-energy gravitates, including gravitation itself. This is really unavoidable for a theory in which the metrical relations between entities determine the "positions" of those entities, and those positions in turn influence the metric".
This non-lineraity means also, as we will see later, that two gravitons are able to exchange a graviton, which would not be possible in the case of a set of linear equations; for example, electromagnetism's linearity does not allow two photons to exchange another (virtual) photon to interact.
Remark 4: Finally and to be accurate, the EFE do NOT determine completely and uniquely all ten components of the metric. The Einstein equation must place only six independent constraints on the ten gμν(P), leaving four arbitrary functions to be adjusted by man's specialization of the four coordinate functions xα(P). The fact that ten distinct differential equations lead to the setting of only six constraints is precisely due to the null divergence of the Einstein tensor G.

