Einstein's journey to Special Relativity was triggered by a simple question: what would it mean if the speed of light were the same for all observers?
The start of his long and tortuous journey to General Relativity began with an equally simple observation: in a gravitational field and in the absence of air resistance, all things fall to the ground at the same rate of acceleration, regardless of their mass. That's it...!
The weak equivalence principle (WEP)
Formulated in a more precise way, Einstein assumed the correspondence between inertial mass, which appears in Newton's F= ma and describes how difficult it is to accelerate an object and (passive) gravitational mass, which describes the strength with which gravity acts (that is the so called weak version of the Equivalence Principle)
Actually, if we have an object with inertial and gravitational masses m and M, respectively, and if the only force acting on the object comes from a gravitational field g, combining Newton's second law and the gravitational law gives the acceleration

and if we postulate m = M, then it follows that a = g.

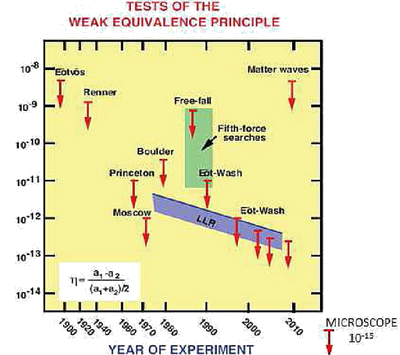
After Galileo, a more precise confirmation of the equality of the two masses came from the austro-hungarian physicist Loránd Eötvös (5×10−9 order of precision)
He measured the torsion on a wire, suspending a balance beam, between two nearly identical masses under the acceleration of gravity and the rotation of the Earth. The idea was that if two bodies were fixed to opposite ends of a rod suspended at it centre by a thin wire, and if they have inequal inertial mass but equivalent gravitational mass, then the attraction of the earth would be the same for both, but the acceleration corrections would be different: then the rod shoud twist.
Currently, as the foundational stone of General Relativity, the Weak Equivalence Principle is being probed in space at the 10–15 level by the MICROSCOPE satellite mission of ONERA and CNES. It is worth pointing out that observation of a deviation of the universality of free fall would imply that Einstein’s purely geometrical description of gravity needs to be completed or amended.
Below a synthetic diagram of all the tests of WEP throughout the 20th century:
On the same subject, the video of Apollo 15 commander David Scott, who in 1971, dropped a feather and a hammer in the high vacuum of the lunar surface is also spectacular and is worth watching! (with a funny analysis as a bonus..)
The strong equivalence principle
If we are in a laboratory on Earth, a mass that is released will fall, or accelerate, downward due to the gravitational attraction of the Earth with a rate of acceleration g = 9.80665 m/s2.
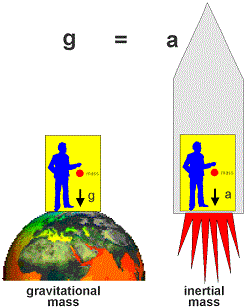
Now, let us move this laboratory into space, away from the gravitational influence of a planet. We now take the same object and release it within an accelerating rocket, of which the level of acceleration, a, is the same as the Earth gravity, g.
In such a situation the rocket will 'push' onto the laboratory floor and move this floor towards the 'falling' mass. As far as the observations of the two motions of the mass relative to the floor are concerned, the accelerated motion in the two cases will be exactly the same. If the laboratory would have no windows, the observer could not distinguish between an acceleration due to gravity (e.g. on Earth) and an acceleration due to a 'push' of e.g. a rocket in space[1].
Inversely, if gravity and acceleration are equivalent, we should be able to 'cancel' the effects of gravity by choosing a referiential in free-fall: locally, this referential becomes inertial and the special relativity holds true for its coordinate system.
In a lift in free fall, provided that an observer makes observations only in a local spacetime neighbourhood, there is are no experiments that he can do inside the lift that are able to distinguish between the possibilities that he is plummeting toward earth or floating in outer empty space.
This kind of tiny free falling lifts or frames are referred to as Local Inertial Frame (LIF), and will turn out to be of major importance in the development of general relativity.
Actually, Einstein referred to this 'reduction' of the physics of curved/gravitationnal spacetime over small free falling/flat regions to the physics of special relativity as "the happiest thought of his life".
Thus Einstein did suggest a sense in which his ideas on gravitation 'generalized' the theory of relativity, i.e a way in which the Principle of Equivalence could generalize the Principle of Relativity.
For if an unaccelerated frame of reference subject to a homogeneous gravitational field is physically equivalent to an accelerated frame, then, at least when there is gravitation, it seemed to Einstein that there is no such thing as absolute acceleration.
Just as the special theory eliminates absolute velocity, its generalization through the principle of equivalence eliminates absolute acceleration.
You can watch this very well made video from Dr Physics A for an introduction to Equivalence Principle
General Relativity: An Introduction - Part 1 of 2
General Relativity: An Introduction - Part 2 of 2
[1] We should note that assimilating a referential at rest on Earth to an accelerating referential in empty space is another way of disqualifying it as a proper inertial referential. We could refer also to our article Inertial Frame of Reference where a referential on Earth was already considered as a non inertial frame because of the Coriolis force.

