It's important for us to understand what Christoffel symbols do exacly mean from a physical point of view, as we know that in General Relativity, the paths of particles and light beams in free fall are calculated by solving the geodesic equations in which the Christoffel symbols explicitly appear (refer to Geodesic equation and Christoffel symbols)
In many applications, it is important to know how a vector fiels changes as we move from one location to another.
For vectors expressed using Cartesian coordinates, taking the derivative of a vector is quite staightforward: we simply take the derivative of each of the vector's component.
Let's consider a vector field V (x,y, z) representing air moving in a room. We can imagine an arbritrary function describing our vector field:
V = (3xy) êx + (x+ 4y + 3z) êy + (2y) êz
If we now are asked to find the rate of change of the air with respect to the (x, y, z) coordinates system, we could easily take the partial derivates of V:
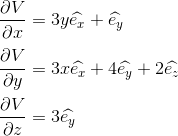
Here we don't need to worry about differentiating the basis vectors êx, êy, êz because they are constant, each is one unit long and pointing along the x, y, z axis respectively.
But here is the crux of the problem: in most of the coordinate systems (the exception being when we are using Cartesian coordinates in the Minkowski space of special relativity), because the basis vectors point in different directions as we move around the space, we must also consider the derivatives of the basis vectors.
So if we consider a vector V = Vαeα , the exact derivative should give us:
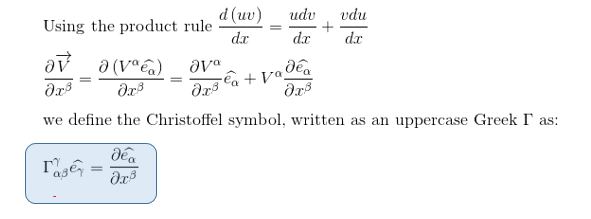
In which the index α specifies the basis vector for which the derivative is being taken, the index β denotes the coordinates being varied to induce this change in the αth basis vector, and the index γ identifies the direction in which this component of the derivatives points:

The example that follow in polar coordinates should help make the things clearer
This equation should be read as follows: the change in er caused by a change in θ has zero magnitude in the er direction, and the change in er caused by a change in θ varies inversely with distance in the eθ direction.

We recall from our article Geodesic equation and Christoffel symbols that the Christoffel symbol can be calculated during a transformation from one referential ξα to xα also as
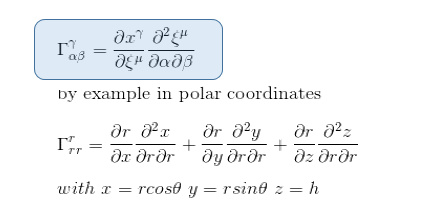
You can refer to the article Christoffel symbol exercise: calculation in polar coordinates in which we are calculating all the Christoffel coefficients in polar coordinates for a two-dimensional Euclidean space.
Finally, the Christoffel symbols have the following characteristics:
- they are symmetric on the lower indexes, i.e Γγαβ = Γγβα (that's evident from the above definition) [1]
- at each point of a N-dimensional spacetime, as each of the three indices (lower and upper) can take N values, N x N x N Christoffel symbols will be defined.
- in a four-dimensionnal coordinate system, 4x4x4 = 64 different Christoffel symbols should theoretically been defined, but because of the lower indices symmetry, and as there are only 10 different ways to arrange 4 coordinates if the permutations are equivalent - nx(n+1)/2- , we finally get only 4x10 = 40 distinct values.
[1] From a more mathematical perspective, these Christoffel symbols called of the 'second kind' are the connection coefficients—in a coordinate basis—of the Levi-Civita connection and since this connection has zero torsion, then in this basis the connection coefficients are symmetric.

