Gravitational redshift Part II - Derivation from the Equivalence Principle

By applying the Equivalence Principle, Einstein was able to obtain important results of the general theory of relativity even before he could solve the corresponding field equations.

You can read this demonstration in the 1907 article On the relativity Principle and the conclusions drawn from it". Actually, as outlined in our article 1907 Equivalence Principle first published mention, the equivalence of gravitation and acceleration is mentionned there for the first time by Einstein.

We will try to demonstrate that the gravitational redshift , i.e the fact that the light freqency changes when entering or leaving a gravitational field - which has been derived from the metric tensor in Newtonian limit in the previous article, could also be derived from this principle of Equivalence.

Consider light traveling from the bottom to the top of a rocket undergoing constant acceleration a. Let point A be at the bottom of the spacecraft, and point B at the top.  The separation distance measured in the reference frame of the rocket is H.

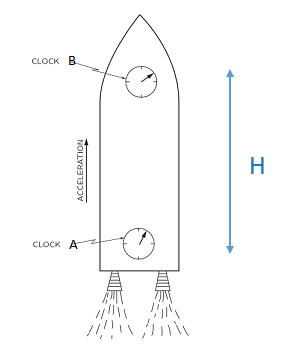
When light first leaves point A, the velocity of the rocket is v_A with respect to another reference frame (the Earth, for example), and  let's call T the time  for light to travel to point B, so:

• v_A = velocity of the rocket when light is emitted at point A
• v_{B =} v_A + aT = velocity of the rocket when light reaches point B

The time T for light to reach B (from the Earth perspective) is:

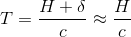
we approximate T to H/c as we consider a << c ('small' acceleration)

Also the change in velocity of the rocket between emission and reception is: