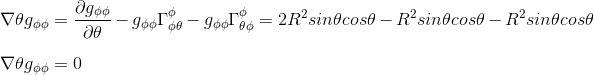Covariant differentiation exercise 2: calculation for the Euclidean metric tensor

In the precedent article Covariant differentiation exercise 1: calculation in cylindrical coordinates, we have deduced the expression of the covariant derivative of a tensor of rank 1, i.e of a contravariant vector - type (1,0) or of a covariant vector - type (0,1).

It can be shown that the covariant derivatives of higher rank tensors are constructed from the following building blocks:

• - take the partial derivatives of the tensor
• - add a Γ^α_γβ term for each upper index
• - substract a Γ^γ_αβ  term for each lower index

 Following the three rules given above, we obtain for tensors of rank 2, respectively of type (1,1) T^μ_ν , (0,2) T_μν and (2,0) T^μν:

We recall from our article Minkowski's Four-Dimensional Space-Time the Euclidean metric tensor's expression  for Cartesian coordinates

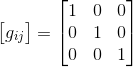
 And substituting g_ij in the second above equality dedicated to type (0,2) tensor gives

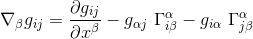
 As all the terms g_ij are constant, the first term δg_ij/δx^β is null. And because there is no curvature in the Euclidean space, all the Christoffel symbols vanish, so that the conplete right-hand side of the equation equals zero, and therefore

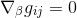
But this is the magic and clever thing about tensors, if this equation holds true in a particular coordinates system, here the Cartesian coordinates, it must be true for the Euclidean metric in ALL coordinate systems.

Covariant derivation of the Euclidean metric in spherical coordinates

Let's try to verify this by calculating one component of the covariant differentiation in the spherical coordinates.

We recall from our article that in spherical coordinates, the metric's expression is

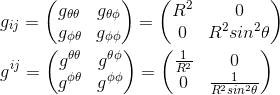
If we were to calculate the component g_ΦΦ;θ, we should then write

But g_αφ !=0 only if α = φ, based on the above expression, so we can simplify this equation

Or

 And from previous article Christoffel symbol exercise: calculation in polar coordinates part II, we know the expression of the Christoffel symbols Γ^Φ_θΦ = Γ^Φ_Φθ = cosθ/sinθ

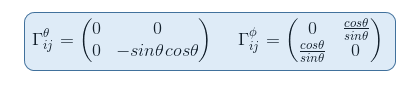
 so that

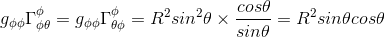
Finally, we confirm that this component of the covariant derivative with respect to θ equals also zero in a polar coordinates system, as expected