To make the meaning of the equations of covariant differentiation seen in last article Introduction to Covariant Differentiation more explicit, we will consider the covariant derivative of vector V with respect to θ in cylindrical coordinates (so x1=r, x2=θ, and x3=z).
Setting β=2 in the following equation, since we are interested in the covariant derivative with respect to θ:
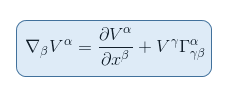
we get
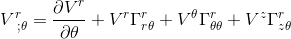
We know the values of the first two Christoffel symbol as we have already calcuted them in the previous article Christoffel symbol exercise: calculation in polar coordinates part I
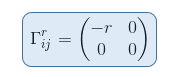
so that we already know that
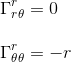
We know also that since
all the symbols from the following form vanish
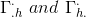
thus we end up with this equality
which says that a change in the r-component of vector V caused by a change in θ is caused both by a change in Vr with respect to θ and by a change in the basis vectors which causes a portion of V that was originally in the θ-direction to now point in the r-direction.
Likewise, for the change in Vθ as the value of θ is changed, we have
which says that a change in the θ-component of vector V caused by a change in θ is caused both by a change in Vθ with respect to θ and by a change in the basis vectors which causes a portion of V that was originally in the r-direction to now point in the θ-direction.
Thus finally the covariant derivative of vector V with respect to θ in cylindrical coordinates is
