Empty spacetime is flat - it looks exactly like the Minkowski's spacetime of Special Relativity.
In Einstein's geometric General Theory of Relativity, a mass - or equivalently energy - that we place in an region of space will lead to a distortion of space-time, commonly referred to as spacetime curvature.
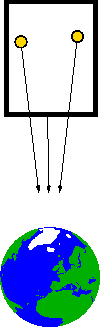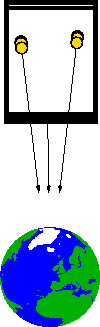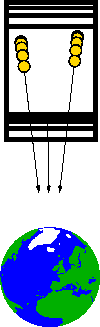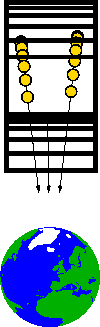
In curved space-time, there are no straight lines - just as there are no straight lines on the surface of a sphere. The closest we can get to the notion of a straight line is a geodesic, a spacetime curve that is as straight as possible.
The tendency of objects in free-fall along a geodesic to approach or recede from one another, in other words, the fact that the initially parallel geodesics of two objects deviate from each other - referred to as geodesic deviation, is the signature of a curved spacetime.
Another way of measuring spacetime curvature is by parallel transporting a vector (moving a vector along a path, keeping constant all the while). See the article Riemann curvature tensor part I: derivation from covariant derivative commutator where we are deriving the curvature by using the covariant derivative commutator.
Mathematically, this curvature information is encoded into the Riemann tensor: if only one component of this tensor is non-zero, then the corresponding spacetime is curved.
Refer to the article The Riemann curvature tensor part II: derivation from the geodesic deviation for the demonstration.
Refer to the article Newtonian limit to evaluate the spacetime curvature on Earth.
Refer to the legendary Feynman's lecture on Curved Space for a general introduction.

