In the previous article The Riemann curvature tensor part I: derivation from covariant derivative commutator, we have shown a way to derive the Riemann tensor from the covariant derivative commutator, which physically corresponds to the difference of parallel transporting a vector first in one way and then the other, versus the opposite.
Another interpretation is in terms of relative acceleration of nearby particles in free-fall.
Imagine a cloud of particles in free-fall. Let us suppose that an observer is travelling with one of the particles, and that he looks at a nearby particle and measures its position in local inertial coordinates. In special relativity, it will move in a straight line at constant speed with no acceleration. But what happens in a gravitational field?
As we recall from our article Geodesic equation and Christoffel symbols , a geodesic generalizes the notion of a "straight line" to curved spacetime.
Here we will show how the evolution of the separation measured between two adjacent geodesics, also known as geodesic deviation can indeed be related to a non-zero curvature of the spacetime, or to use a Newtonian language, to the presence of tidal force.
So let us pick out two particles following two very close geodesics.
Their respective path could be described by the functions xμ(τ) (reference particle) and yμ(τ)≡xμ(τ) + ξμ(τ) (second particle) where τ (tau) is the proper time along the reference particle's worldline and where ξ refers to the deviation four-vector joining one particle to the other at each given time τ.
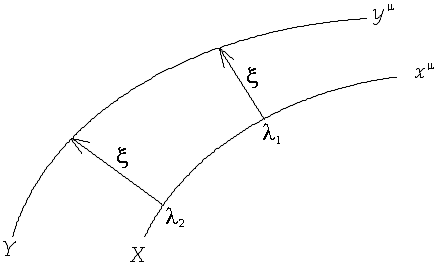
The relative acceleration Aα of the two objects is defined, roughly, as the second derivative of the separation vector ξα as the objects advance along their respective geodesics.
Our goal in this article is to show that this relative acceleration is related to the Riemann tensor by the following equation
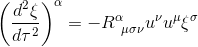
for which a null Riemann tensor leads to a null relative acceleration between the particles, which is equivalent to say that the spacetime is flat.
So lets try to demonstrate it.
As each particle follows a geodesic, the equation of their respective coordinate is:
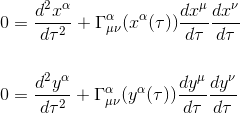
In each of these equations, the Christoffel symbol is evaluated at each particle's x and y respective position. As the separation among particles is infinitesimal, we can therefore evaluate Christoffel symbol at yα(Τ ) position by a Taylor series development.

With the assumption that yα(τ) = xα(τ) + ξα(τ) and by replacing this last expression in the y particle's geodesic equation, we get:
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.
Since this is still a tensor equation, the quantity in brackets is a tensor and we can define the Riemann tensor as the opposite of this quantity
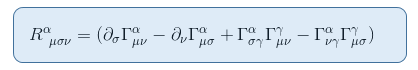
Then we can rewrite the above equation in a shorter expression, known as the geodesic deviation equation
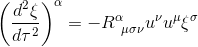
Since the only quantity in this equation that depends intrinsically on the metric is the Riemann tensor, we see that if it is identically zero, spacetime is flat, but if only one component of this tensor is non-zero, spacetime is curved.
We’ll explore some more properties and examples of the Riemann tensor in future posts.

