In our previous article Introduction to quantum computing, we saw that the real value of quantum computing lies in the fact that a quantum system can do processing while the qubits are in a superposition state. Hence, the operations defined by the quantum algorithms do not manipulate by example just 3 bits, they manipulate 23 probability[1] values. One step in a quantum algorithm on a quantum computer with 3 qubits is therefore modifying 8 values. Adding one qubit doubles the processing capabilities of the quantum computer. This explains the term "exponential" that is often used together with quantum computing: adding N qubits adds processing power proportional to 2N .
If it should be clear by now that a quantum computer allows some kind of parallel processing, what does we mean more precisely by processing a qubit?
In classical computing, all the operations finally come down to a sequence of simple manipulations of the bits in the computer systems. Those low-level operations are achieved using gates. It can be shown that with a limited number of gates, all possible scenarios can be achieved.
A very simple classical gate is the NOT gate, also known as the inverter.This gate has one input bit, and one output bit. The output bit of the gate is the inverse of the input bit. If the input is "0", the output will be "1". If the input is "1", the output will be "0".
The behavior of gates is often explained via simple tables where the possible combinations of input bits are listed, and the resulting output is listed in the last column. The following table shows the behaviour of the NOT gate

When the input of the gate is '0', the output is '1'. When the input of the gate is '1', the output is '0'.
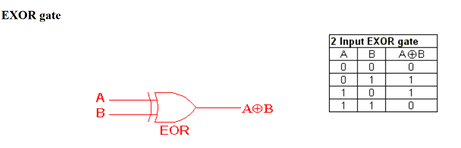
The NOT gate involves a single bit only, but other gates involve more bits. The XOR (or EXOR) gate , for example, takes the input of 2 bits, and outputs a value that is '1' in case exactly one of the 2 input bits is 1 and the other is '0'.
Quantum gates
If we want to process data in quantum computing, we have to use gates as well. Quantum gates are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.
But unlike many classical logic gates, quantum logic gates sould be reversible. That is, it should always be possible to apply another gate and go back to the state of the system before the first gate was applied. This restriction does not apply on classic gates. For example, the XOR gate is not reversible. If the result of an XOR gate is '1', it is impossible to know whether the first bit was '0', or whether it was the second bit[2].
In this article, we will only focus on quantum gates applying to single bits. We will present the quantum equivalent of the XOR gate in a later article, C-NOT gate, Bell State and Entanglement.
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.

