After having introduced the basic concept of entanglement in our previous post Introduction to quantum entanglement by considering a composed system made up of a coin and a dice, let's consider a new more realistic system built up from two spins - each spin is attached to a a particule at a different space location.
Alice has a set of spin operators, labeled σA, that act on her system and Bob has a similar set for his system, which can be labeled σB, so we don't mix them up with Alice's ones.
Each operator/apparatus can be independently oriented along any axis, so that the full set of components for Alice's and Bob's are: σAx, σAy, σAz and σBx, σBy, σBz
Knowing that any vector of a given Hilbert space can be expressed in any orthonormal basis, let's choose the basis along the z axis. Along this axis, each spin can be either in up state |u> or in down state |d>.
As per our previous article, the basis vectors are nothing else than the tensor product of the basis vectors of each sub-space, ie the tensor product of ΗA = {uA, dA} x HB = {uB, dB}:
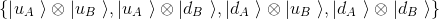
which can be also written in a more abbreviated way as
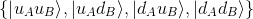
We know that the simplest state for the composite system is a product state (the result of completely independent preparations by Alice and Bob) and is of the form:
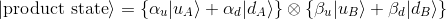
where the left factor represents Alice's state and the second factor represents Bob's.
We recall also from our basic quantum mechanics lesson how the spin operators act on the distinct states of a single spin

This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.
More generally, we could demonstrate that for any single state or product state, the following equation holds true:
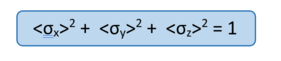
In the next article, we will calculate the expectation value of σ for an entangled state. Would we get the same results?
[1]Such a state is said to be pure: a pure quantum state is a state which can be described by a single ket vector (in a two-dimensionnal Hilbert space in our case)
[2]If you don't remember the expectation value of an observable A for any given |state> is defined as
<A> = <state|A|state>
[3]We will show that in a next article when we will build tensor products from component matrices.

