In this article, our goal is to show that the geodesics for a two-dimensional Euclidean space are straight lines.
In Cartesian coordinates and in two dimensional space, as there is no z coordinates, the Euclidean line element there becomes:
dl2 = dx2 + dy2
Therefore, the corresponding metric is - we are using Latin indices as we are not working in spacetime:

We also know from our previous article Geodesic equation and Christoffel symbols that the geodesic equation can be written as
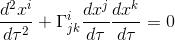
But the Proper time is clearly not a convenient parameter in the case of the propagation of photons (the proper time is not defined for massless particles)
We should better use a so called affine parameter λ, as per below:

In order to calculate the eight Christoffel symbols (2*2*2 in 2D space), we need to use the equation given in Christoffel symbols in terms of the metric tensor
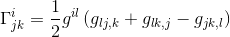
But as the values of the metric are constant (equal to 0 or 1 as pointed out above), the partial derivatives gij,k = 0 for all values of i, j and k. Therefore Γjki = 0 for all values i, j, k and the geodesic equation simply becomes :
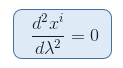
The function xi = aλ + b where a and b are constants is obviously a solution to this equation as when derived twice it gives 0.
As we are using Cartesian coordinates where xi equals x and y, the above equation becomes then
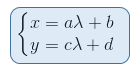
Solving for λ gives:
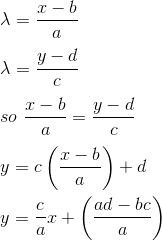
which is the equation of a straight line with gradient c/a and constant (ad-bc)/a.

