Dans cet article, on se propose de dériver la formulation exacte de l'énergie relativiste, dont on avait obtenu une approximation dans le cas des vitesses faibles dans l'article Introduction à E = mc2 (façon Feynman).
En fait, l'énergie - comme la quantité de mouvement - est une quantité conservée et représente l'hamiltonien du système. Celui-ci s'exprime en fonction du lagrangien et sa formulation pour une particule en mouvement est la suivante:
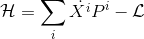
avec Xi (X1,X2,X3) et Pi représentant respectivement les coordonnées et les moments de la particule.
Nous savons déjà d'après les deux articles précédents que les composantes de la quantité de mouvement relativiste s'écrivent:
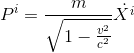
Nous connaissons également la formulation relativiste du lagrangien relativiste, comme déduit dans Action relativiste
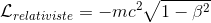
Nous avons donc toutes les informations nécessaires pour développer l'hamiltonien:
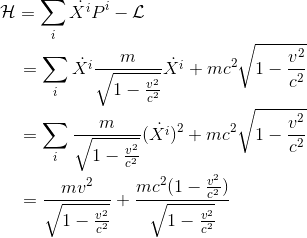
Soit finalement en simplifiant par mv2 au numérateur:
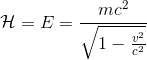
Cette équation est la formule générale de l'énergie d'une particule de masse m en fonction de sa vitesse v.
Dans le cas où les vitesses sont faibles par rapport à celle de la lumlère, on obtient en nommant m0 la "masse au repos", l'énergie totale de la particule égale à l'énergie cinétique (comme dans la formule non relativiste) plus un nouveau terme, l'énergie de masse[1].
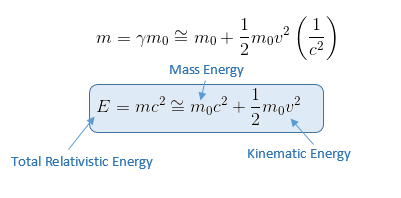
Mais plus généralement, l'énergie cinétique Ec n'est pas déifnie par 1/2mv2 mais par la partie de l'énergie relativiste totale qui ne dépend que de la vitesse:
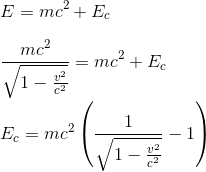
[1] En raison de la valeur de c, cette énergie de masse est énorme si on la compare par exemple à son énergie cinétique pour une vitesse classique à une vitesse v<<c. Ainsi, un kilogramme correspond à autant d'énergie que celle que produirait un réacteur nucléaire de puissance 1 GW pendant trois ans.

