Dans l'article précédent, nous avons déduit l'énergie relativiste pour une particule de masse m.
Cependant, on constate clairement que cette formule n'est plus valable pour une particule de masse nulle, puisqu'à la fois le numérateur et le dénominateur tendent chacun vers zéro, et zéro sur zéro ne donne pas quelque chose de déterminé.[1]
L'astuce ici consiste à tenter de lier ensemble les deux quantités que l'on a considérées dans nos articles précédents, à savoir l'énergie E et la quantité de mouvement P.
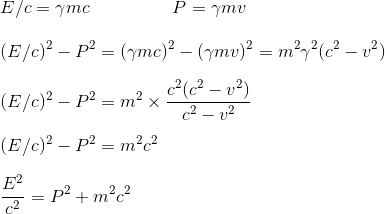
Soit finalement l'expression de l'énergie totale d'une particule
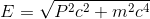
L'équation que l'on vient d'obtenir exprime l'énergie en fonction de la quantité de mouvement et de la masse. Elle s'applique à toutes les particules, qu'elles soient de masse nulle ou non. Grâce à cette formule, nous pouvons voir immédiatement voir quelle est la limite lorsque la masse tend vers zéro.
Avec m=0, le second terme de la racine carrée s'annule, et la racine carrée de P2c2 est simplement égale à la nome de P multipliée par c[2].
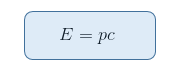
Remarque importante: Nous verrons plus tard que la quantité (E/c)2 - P2 n'a pas été choisie par hasard mais constitue le produit scalaire de l'équivalent relativiste du vecteur quantité de mouvement en mécanique classique: le vecteur quadri-impulsion ou quadri-quantité de mouvement.
[1] Dans l'état actuel de nos connaissances, le photon et les gluons, les particules responsables de l'interaction entre les composants des nucléons nommés quarks, sont les seules particules observées dénuées de masse. Mentionnons tout de même que si l'interaction gravitationnelle est elle aussi associée à une particule dans le cadre d'une description quantique, l'hypothétique graviton, les théories admises de nos jours suggèrent qu'elle serait également de masse nulle.
[2] La physique quantique décrit de manière complémentaire l'énergie E d'une particule de masse nulle en la reliant à la fréquence ν de l'onde qui lui est associée, par exemple pour un photon de couleur donnée. L'équation de Planck-Einstein proposée par Einstein pour les photons, indique ainsi qu'ils vérifient E=hν où h=6.62x10-34 J.s est la constante introduite en 1900 par Max Planck (1858-1947) et qui porte depuis son nom.

