Dans cet article, on se propose de retrouver la formulation relativiste de la quantité de mouvement, non pas à partir du lagrangien comme dans l'article précédent Quantité de mouvement relativiste, mais à partir d'un cas plus concret de collision entre deux particules.
Reprenons l'exemple du choc inélastique présenté dans notre article en version anglaise Introduction to Four-momentum vector and E = mc2
Dans un référentiel R, on considère deux particules lancées l'une vers l'autre sur un même axe avec la même vitesse rectiligne uniforme v, et se percutant pour finalement s'assembler dans un seul et unique objet immobile dans ce même repère R.
Nous considérons également le même choc mais à partir d'un référentiel R' attaché à l'une des deux particules en mouvement et tâchons de calculer la quantité de mouvement avant et après le choc inélastique dans chacun de ces référentiels.
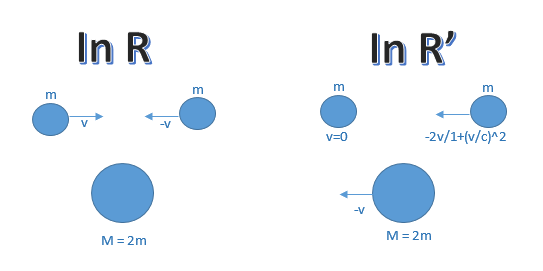
Considérons d'abord l'hypothèse d'une masse constante (indépendante de la vitesse de la particule)
Dans le référientiel R, calculons les quantités de mouvement avant et aprés le choc:
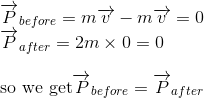
SI à présent on se place dans le référentiel R' attaché à la particule initialement en mouvement vers la droite dans le référentiel R, on se souvient que la vitesse de la particule de droite ne s'additionne pas selon la transformation galiléeene v=-(v+v), mais s'exprime plutôt selon la formule relativiste de composition de vitesse vue dans notre précédent article Transformations de Lorentz III - Cinématique relativiste - Composition des vitesses.
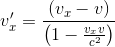
Soit dans notre cas on posant vx=-v puisque la particule de droite se déplace vers la gauche, on obtient:
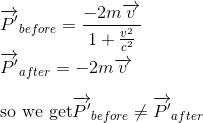
Clairement, notre hypothèse d'une masse relativiste constante doit être fausse, puisqu'elle n'assure pas la conservation de la quantité de mouvement dans ce cas simple de collision inélastique.
Considérons à présent l'hypothèse d'une masse non constante (dépendante de la vitesse de la particule)
Faisons la double hypothèse de:
- la conservation de la masse relativiste
- la conservation de la quantité de mouvement
et voyons à quoi cela nous mène.
Dans le référentiel R', nous avons la double égalité suivante,
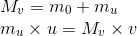
en posant u = la vitesse relativiste de la particule de masse mu de droite, soit comme on vient de le voir plus haut:
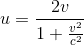
En éliminant Mv des deux équations précédentes, on a:
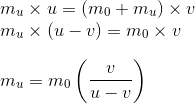
En se rappelant la valeur de u:
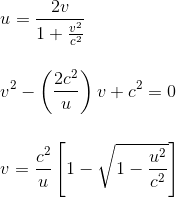
Remarque: dans l'étape précédente, on a choisi la solution de l'équation du second dégré avec le signe -, car lorsque l'on fait tendre u->0, on doit avoir un résultat fini pour la vitesse v.
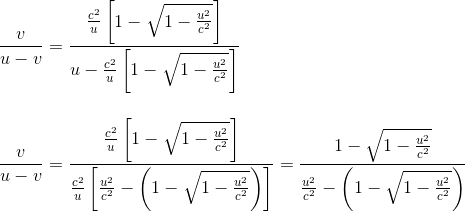
Tâchons encore de simplifier cette expression:
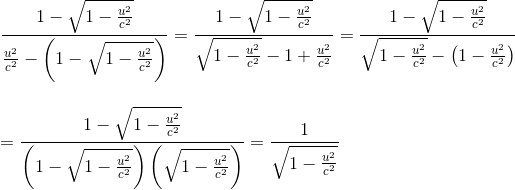
On retrouve bien le résultat admis avecFeynman au début de notre article Introduction à E = mc2 (façon Feynman), on a:
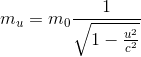
Et l'on retrouve donc notre formule de la quantité de mouvement relativiste
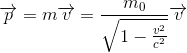
CQFD

