La quantité de mouvement est un concept central en mécanique, avec la propriété fondamentale d'être conservée[1] dans un système fermé.
En mécanique classique, la quantité de mouvement se définit comme la dérivée du lagrangien par rapport à la vitesse. Exprimée par ses composantes (Px, Py, Pz) , on a donc:
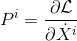
Pour trouver l'expression relativiste de la quantité de mouvement d'une particule, il nous suffit d'appliquer le lagrangien relativiste tel qu'exposé dans l'article précédent Action relativiste
Par exemple, si l'on considère la composante selon l'axe x de la quantité de mouvement Px, on a:
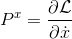
En calculant la dérivée on obtient:

En considérant les composantes Py et Pz de la quantité de mouvement, on trouverait exactement de la même façon:
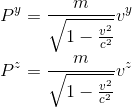
On remarque la similitude de la quantité de mouvement relativiste avec son pendant classique. Comme on en avait fait l'hypothèse avec Richard Feynman dans notre précédent article Introduction à E = mc2 (façon Feynman), il suffit de remplacer la masse au repos utilisée en mécanique classique par son pendant relativiste, donc la multiplier par le facteur de Lorentz[2]
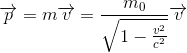
[1] En fait, la quantité de mouvement apparaît naturellement en mécanique comme la grandeur conservée associée à l'invariance par translation dans l'espace du Lagrangien (ou du Hamiltonien), c'est-à-dire à la propriété d'homogénéité de l'espace grâce au théorème démointré en 1915 par la mathématicienne allemande Emmy Noether et selon lequel toute symétrie continue de l'action implique la conservation d'une quantité associée.
[2] Comme on pouvait s'y attendre, les formules relativiste et non relativiste de la quantité de mouvement se confondent lorsque la vitesse est beaucoup plus petite que celle de la lumière, auquel cas le facteur de Lorentz tend vers 1.

