In our previous article Introduction to Four-velocity vector, we have presented the spacetime velocity vector equivalent to the classical three dimensional velocity vector.
The next logical question should be: what could be the expression of the spacetime momentum vector?
Why the spacetime four-momentum could not be the old fashioned classical one
Let's be naive and suppose first that our spacetime momentum vector could be written as p = mv with v the classical newtonian velocity vector.
Let us consider what is commonly called an inelastic collision, i.e. two objects of the same kind, moving oppositely with equals speed v, hit each other and stick together, to become some new, stationary object (to help visualize this, we can imagine the two particules as being chewing gums...).
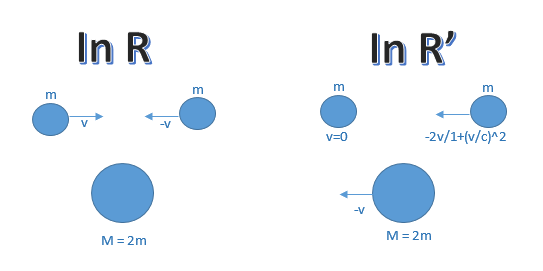
Let us estimate the momentum of the system before and after the collision in referentials R and R', with R' attached to the first left particule.
In referential R:
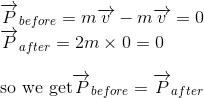
In referential R', the important thing to remember is that the relative speed of the right ball with respect to the speed of the left ball is NOT -v-v = -2v because in special relativity, as seen in our last article Introduction to Four-velocity vector, the velocity do not transform according to Galilean answer, but according to the following expression, with v being the relative speed of the referentials.
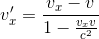
So in our case, in R' referential, we can write:
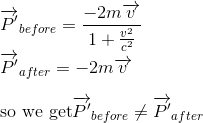
Obviously, as momentum must be conserved in all referentials[1], our hypothesis was wrong, and the relativistic momentum could not equal the particle's mass m multiplied by its ordinary spatial velocity v, as it is defined in Newtonian mechanics.
Four momentum definiton and space time representation
It would be certainly a good idea to multiply the four-velocity by the rest mass m of a particle to get our four-momentum definition:
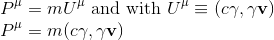
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.
Energy-momentum relation
We still have to elucidate a last question: the total relativistic energy's formula and the mass-energy equivalence equation we have established before can not apply to massless particule such as photons.
From above, we know that the norm of the four momentum is a constant in all inertial frames equals to rest mass x c = m0c.
But we know also from the precedent paragraph that the time component of the four-moment vector γm0c could be expressed also as E/c as we know that total relativistic energy E = γm0c2
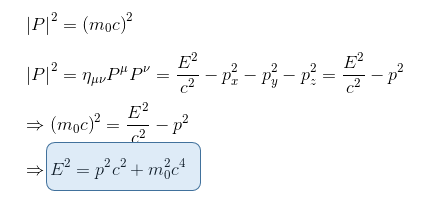
And for a photon, which has zero 'rest mass' but still does have energy and momentum, we get
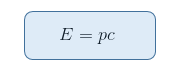
which describes the energy-momentum relation for a photon.
As the energy of a photon is given by E = hc/λ, where h = 6.63x10-34Js (Planck's constant) and λ is the wavelength, we can easily calculate for example the momentum of a photon of blue light, which has a wavelength of 450nm
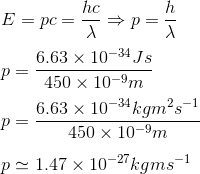
[1] Should it not be the case, then the fundamental Principle of Relativity would be violated, as we would have a way to distinguish a 'rest' frame where the conservation of momentum law would be valid (our referential R above) from a 'moving' frame where this law would not hold (our R' referential).
[2] Richard Feynman SIx-Not-So-Easy pieces Chapter 3 - The special Theory of Relativity §3.8 Relativistic dynamics

