As we know from the Newton's first law of motion, a free particle in motion travels in a straight line with constant velocity.
In this article our aim is to express this law, sometimes referred to as the law of inertia in the terms of special relativity's concepts. More precisely, we will try to demonstrate that in special relativity's Minkowski flat spacetime, a free particule has the maximum proper time of all possible world lines that connect two events.
As a starting point, let us recall the expression of the Proper Time as measured by a clock between two events A and B in any inertial referential, with t and v correponding respectively to the time and the speed of the clock as measured in this referential - here we assume c=1 for more readability:
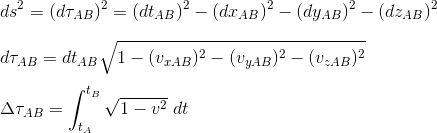
If we draw the wordline of a given free particule moving from an event A to an event B in its rest inertial frame (xAB=yAB=zAB=0), it corresponds then to the t-axis, and we have ΔΤAB(Inertial) = ΔtAB (proper time equals coordinate time).

Now let us consider another non-free particule, following in this case a non-inertial wordline between the two identical events A and B: this time, the world line will be some path that can wander around any way it likes (as long as its speed doesn’t exceed 1), provided that it comes back to meet the first particle at event B. At least for some time, this particle should have a not-null speed in the inertial referential attached to the first particule (as the x-component of the speed is at each time given by the inverse of the world line slope in the spacetime diagram).
We get then ΔΤAB(Non-Inertial) < ΔtAB
As this could be generalized for any events A and B, any word line of a free particule and any other world line connecting these two events, we can generalize this result by saying that an object always moves from one place to another so that a clock carried on it gives a longer time than it would on any other possible trajectory. In free motion, the trajectory makes the proper time of an object a maximum.
Remark: To fully satisfy ourselves that there is no paradox, we should also see how things look from the viewpoint of a virtual observer attached to the non-inertial particle which is wandering around. For her, the free particle is the one doing a random motion while she snakes along her own time axis. It looks like we have a paradox here - similar to the so called Twin paradox. Since the non-free particle is at rest in its own referential, it seems that the clock attached to it should speed maximally through time and hence age the most.
Actually there is no paradox there as the non-free particle is attached to a non-inertial, accelerating referential. In this case, the assumption that spacetime is unchanging and the same everywhere that we used to write down the equation is wrong. To be a little bit more specific and without going into too many mathematical details, the upshot is when the non-free particle turns around and accelerates, the free particle ages rapidly relative to it, and that more than makes up for the fact that she ages more slowly during the non-accelerating phases of the motion. There is no paradox.

