In non-relativistic physics, the velocity of an object is a three dimensional vector whose components give the object’s speed in each of three directions (the directions depend on the coordinate system).
The path of a particle moving in ordinary three-dimensional Euclidean space can be described using three functions of time t, one for x, one for y and one for z. The three fuctions x=f(t), y=f(t), z=f(t) are called parametric equationsand give a vector whose components represent the object's spatial velocity in the three x,y,z directions.
The spatial velocity of the particle is a tangent vector to the path and can be written as:
Four-vector
In special relativity, a four-vector A is a vector with a "timelike" component and three "spacelike" components, and can be written in various equivalent notation[1]
More precisely, a point in Minkowski space is a time and spatial position, called an Event, or sometimes the position four-vector or four-position or 4-position, described in some reference frame by a set of four coordinates:
where r is the three-dimensional space position vector. If r is a function of coordinate time t in the same frame, i.e. r = r(t), this corresponds to a sequence of events as t varies. Also the definition x0 = ct ensures that all the coordinates have the same units (of distance). These coordinates are the components of the position four-vector for the event.
Generally speaking mathematically, one can define a 4-vector a to be anything one wants, however for special relativity between one Inertial Frame of Reference and another, our 4-vectors are only those which transform from one inertial frame of reference to another by Lorentz transformations.
Four-velocity vector
The vector that represents the relativistic counterpart of velocity, which is a three-dimensional vector in space, is a four-vector and is called the Four-velocity vector.
As we have seen in Proper time, a clock fastened to a particle moving along a world-line in four-dimensionnal spacetime will measure the particle's proper time τ and therefore it makes sense to use τ as the parameter along the path. The four-velocity of a particle is then defined as the rate of change of its four-position with respect to proper time, and is also the tangent vector to the particle's world line
To determine the components of the four-velocity vector, we recall that a process that takes a proper time ΔΤ in its own rest frame has a longer duration Δt measured by another observer moving relative to the rest frame, i.e
Δτ = (Δt / γ)
Taking the derivative with respect to propert time, we can then rewrite that:
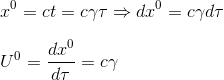
We can use the chain rule to find the spatial components of Uμ for μ = i = 1,2,3:
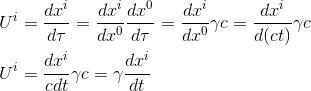
But dxi/dt is the particle's ordinary spatial velocity v = dx1/dt, dx2/dt, dx3/dt = vx , vy, vz so that finally the particle's four-velocity is finally given by:
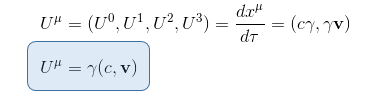
[1] We have already come across this index notation in our article The Lorentz transformations Part IV - Lorentz transformation matrix (tab index notation).
Lorentz transformation
To confirm that this four velocity vector is effectively a four-vector, we have to check that it transforms well under Lorentz transformation.
Let's consider a particule p which has four-velocities U and U' respectively in referentials R and R'
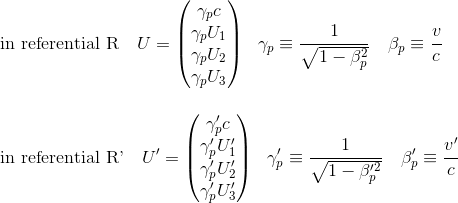
If we assume that the referentials R and R' in standard configuration are animated by a relative velocity vr/r' along the x axis caracterized by a Lorentz factor γ relative to each other, than the Lorentz transformation between the two four-velocities can be written as:
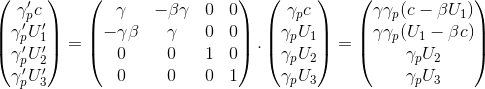
If we consider the two first lines of the matrix product:

Now let's tackle the velocity transformation problem using the Lorentz transformation. If we have two events in spacetime there will be a difference between the corresponding time and spatial coordinates, the intervals Δt, Δx, Δy, Δz.
For example, if we had two events E1=(t1,x1,y1,z1) = (3,1,0,0) and E2=(t2,x2,y2,z2) = (5,4,0,0) then the time interval Δt = 5-3 = 2, and the spatial interval Δx = 4 -1 =3.
We show easily that we get those transformation rules for intervals:

If we bring the two events on the x axis closer and closer together, eventually as Δx and Δt approach 0, the quantities Δx/Δt and Δx'/Δt' become the instantaneous velocities vx and v'x of an object moving through the two events E1 and E2 respectively in referentials R and R'.

We can then confirm that this expression of velocity transformation is strictly equivalent to the one we have found for the x component U1 of the four velocity vector U above.
Similarly, if we consider the components U2 and U'2 along the y and y' axis:
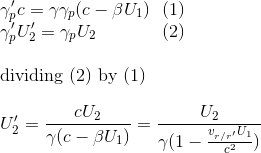
If we use again the Lorentz transformation rules we get:
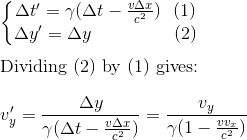
which transfoms exactly as the four velocity U2 component does transform, as expected.
We have just shown that the four velocity vector is defined as a quantity which transforms according to the Lorentz transformation:
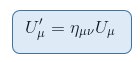
Scalar product
In special relativity the scalar product of two four-vectors A and B is defined by applying the Minkowski metric to the two four vectors, as follow:
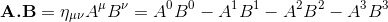
One result of the above formula is that the squared norm of a nonzero vector in Minkowski space may be either positive, zero, or negative.
If A2<0, the four-vector Aμ is said to be timelike; if A2>0, Aμ is said to be spacelike; and if A2=0, Aμ is said to be lightlike. The subset of Minkowski space consisting of all vectors whose squared norm is zero is known as the light cone.
As a direct consequence, the scalar product of the four-velocity vector with itself, i.e. its squared norm is given by:
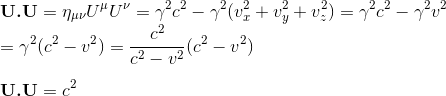
which is obviously an invariant in all the inertial referentials.

